Question

Simplify: -y^3(5y^3-7y-3)

Answer 1

The simplified expression is
`-5y^6 + 7y^4 + 3y^3.`

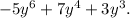
Step-by-step explanation:

In the given expression,
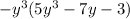`-y^3(5y^3 - 7y - 3)`, we need to distribute the
`-y^3`across the terms inside the parentheses. Applying the distributive property, we get
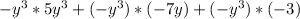`-y^3 * 5y^3 + (-y^3) * (-7y) + (-y^3) * (-3)`. This simplifies to
`-5y^6 + 7y^4 + 3y^3`.

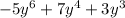In the first term,
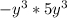`-y^3 * 5y^3`, we multiply the coefficients (-1 * 5) to get -5. Then, we add the exponents of y (3 + 3), resulting in
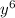`y^6`. So, the first term becomes
`-5y^6`.

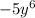In the second term, (
`-y^3`) * (-7y), the product of the coefficients (-1 * -7) is 7, and we add the exponents of y (3 + 1) to get . Thus, the second term simplifies to
`7y^4`.

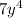Lastly, in the third term, (
`-y^3`) * (-3), the product of the coefficients (-1 * -3) is 3. Since there is no common exponent for y, the term remains as -
`3y^3`.

Putting it all together, the simplified expression is
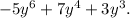`-5y^6 + 7y^4 + 3y^3.` This form is the simplest representation of the original expression, combining like terms and presenting the result in descending order of exponents.