Answer:
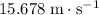 .
.
Step-by-step explanation:
In this question, the rate of change in velocity is given. The speed of the vehicle after travelling the given distance can be found through the following steps:
- Find an expression for speed by Integrating the rate of change of speed
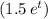 with respect to time.
with respect to time. - Find an expression for distance travelled by integrating speed with respect to time.
- Solve for the time
 required to travel the given distance of
required to travel the given distance of
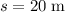 .
. - Substitute the value of
 into the expression for speed and evaluate to find the speed at the given time.
into the expression for speed and evaluate to find the speed at the given time.
To find an expression for speed
 at time
at time
 , integrate the expression for the rate of change in speed with respect to time:
, integrate the expression for the rate of change in speed with respect to time:
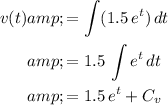 ,
,
Where
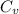 is a constant. Given that the vehicle started from rest,
is a constant. Given that the vehicle started from rest,
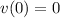 . Make use of this equality to find the value of
. Make use of this equality to find the value of
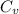 :
:
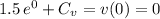 .
.
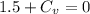 .
.
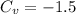 .
.
Hence, the expression for speed at time
 would be:
would be:
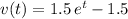 .
.
To find an expression for distance
 travelled at time
travelled at time
 , integrate the expression for speed with respect to time:
, integrate the expression for speed with respect to time:
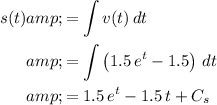 ,
,
Where
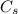 is also a constant. Assuming that the distance was initially
is also a constant. Assuming that the distance was initially
 ,
,
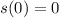 . Solve for the value of
. Solve for the value of
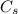 :
:
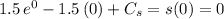 .
.
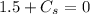
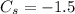 .
.
Hence, the expression for distance travelled at time
 would be:
would be:
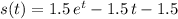 .
.
Assuming that
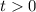 , solve this expression for the value of
, solve this expression for the value of
 that would ensure
that would ensure
 :
:
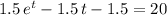 .
.
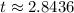 (
(
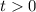 .)
.)
Substitute the value of
 back into the expression for speed to obtain:
back into the expression for speed to obtain:
 .
.
In other words, speed of the vehicle would be approximately
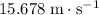 when the distance travelled from the starting position is
when the distance travelled from the starting position is
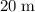 .
.