Question

(2) Use logical equivalences to perform a direct proof that the two following logical statements are equivalent. (20 pts.) Statement 1: (P OR (IP AND Q)) Statement 2: IP AND IQ (3) Prove the following statement using the Direct Method. (20 pts.) If A< B, and B

Answer 1

2) The two statements are not equivalent 3) By transitivity, since A < B and B < C, it follows that A < C

Logical Equivalences:

For Statement 1:
`\( \\eg (P \vee (P \wedge Q)) \)`

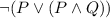
Applying De Morgan's Law:
`\( \\eg P \wedge \\eg (P \wedge Q) \)`

Applying De Morgan's Law again:
`\( \\eg P \wedge (\\eg P \vee \\eg Q) \)`

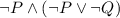
By distributing:
`\( (\\eg P \wedge \\eg P) \vee (\\eg P \wedge \\eg Q) \)`

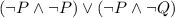
Simplify:
`\( \\eg P \vee (\\eg P \wedge \\eg Q) \)`

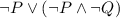
For Statement 2:
`\( P \wedge \\eg Q \)`

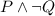
The two statements are not equivalent.

3) Direct Proof:

For the statement "If A < B, and B < C, then A < C":

Assume A < B and B < C are both true.

By transitivity, since A < B and B < C, it follows that A < C

Thus, the statement is proven using the direct method.

Complete Question:

(2) Use logical equivalences to perform a direct proof that the two following logical statements are equivalent. (20 pts.) Statement 1: !(P OR (IP AND Q)) Statement 2: IP AND IQ (3) Prove the following statement using the Direct Method. (20 pts.) If A<B, and B <C, then AC (4) Convert the following from the base