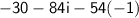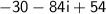Question

Perform the indicated operation. Write the answer in the form a + bi. (-5-91)(6 + 6i) Select one: O a. -84-84i b. 24-84i c. 24 O d. -30 - 541

Answer 1

Hello :)

Answer -

24 - 84i

Step-by-step explanation -

Our task is to multiply these complex numbers:

(-5 - 9i)(6 + 6i)

To multiply, use FOIL.

FOIL = First, Outer, Inner, Last

Multiply the first terms:
`\sf{-5*6=-30}`

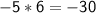
Multiply the outer terms:
`\sf{-5*6i=-30i}`

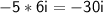
Multiply the inner terms:
`\sf{-9i*6=-54i}`

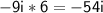
Multiply the last terms:
`\sf{-9i+6i=-54i^2}`

We have:
`\sf{-30-30i-54-54i^2}`

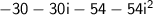
Combine like terms:
`\sf{-30-54i-30i-54i^2}`

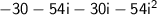
Simplify:
`\sf{-30-84i-54i^2}`

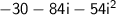
Now, remember that by definition,
`\large\boxed{\sf{i^2=-1}}`!

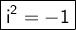Therefore,

`\sf{-30-84i-54(-1)}`

`\sf{-30-84i+54}`

`\sf{24-84i}`

Answer 2

b

Explanation:

product of 2 complex numbers

note that i² = - 1

given

(- 5 - 9i)(6 + 6i) ← expand using FOIL

= - 30 - 30i - 54i - 54i² ← collect like terms

= - 30 - 84i - 54(- 1)

= - 30 - 84i + 54

= 24 - 84i ← in the form a + bi ( with a = 24 and b = - 84 )