Question

For a certain company, the cost function for producing x items is C(x)=40x+150 and the revenue function for selling x items is R(x)=−0.5(x−90)^2+4,050. The maximum capacity of the company is 130 items.

The profit function P(x) is the revenue function R(x) (how much it takes in) minus the cost function C(x) (how much it spends). In economic models, one typically assumes that a company wants to maximize its profit, or at least make a profit!

1. Assuming that the company sells all that it produces, what is the profit function?

P(x)=

2. What is the domain of P(x)?

3. The company can choose to produce either 50 or 60 items. What is their profit for each case, and which level of production should they choose?

4. Can you explain, from our model, why the company makes less profit when producing 10 more units?

Answer 1

`\textsf{1)} \quad P(x)=-0.5x^2+50x-150`

`\textsf{2)} \quad [0, 130]`

`\begin{aligned}\textsf{3)} \quad \sf 50\;items&=\$1,100\\\sf 60\;items&=\$1,050\end{aligned}`

`\textsf{4)} \quad \sf See\;below.`

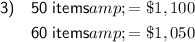
Explanation:

Question 1

The profit function P(x) is given by subtracting the cost function C(x) from the revenue function R(x):

`\large\boxed{P(x) = R(x) - C(x)}`

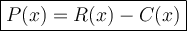
Given functions:

`R(x) = -0.5(x - 90)^2 + 4050`

`C(x) = 40x + 150`

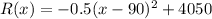
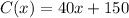
Subtract C(x) from R(x):

`\begin{aligned}P(x) &= (-0.5(x - 90)^2 + 4050) - (40x + 150)\\&= -0.5(x - 90)(x-90) + 4050 - 40x - 150\\&= -0.5(x^2-180x+8100) + 4050 - 40x - 150\\&= -0.5x^2+90x-4050 + 4050 - 40x - 150\\&= -0.5x^2+50x - 150\end{aligned}`

Therefore, the profit function P(x) is:

`\large\boxed{P(x)=-0.5x^2+50x-150}`

`\hrulefill`

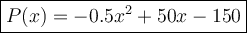
Question 2

The domain of P(x) is the set of all valid values of x for which both the revenue function R(x) and the cost function C(x) are defined.

The variable x represents the number of items.

Given the maximum capacity of the company is 130 items, the domain of P(x) is restricted to:

• Domain of P(x): [0, 130]

`\hrulefill`

Question 3

To find the profit for each case of producing 50 or 60 items, evaluate the profit function P(x) for these values of x.

`\begin{aligned}P(50)&=-0.5(50)^2+50(50)-150\\&=-0.5(2500)+2500-150\\&=-1250+2500-150\\&=1250-150\\&=1100\end{aligned}`

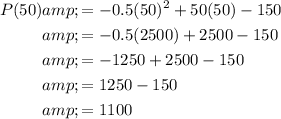
Therefore, the profit when producing 50 items is $1,100.

`\begin{aligned}P(60)&=-0.5(60)^2+50(60)-150\\&=-0.5(3600)+3000-150\\&=-1800+3000-150\\&=1200-150\\&=1050\end{aligned}`

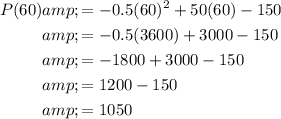
Therefore, the profit when producing 60 items is $1,050.

The company should choose to produce 50 items, since this level of production results in higher profit.

`\hrulefill`

Question 4

The simplified profit function is P(x) = -0.5x² + 50x - 150.

If we convert this into vertex form, we get:

`P(x) = -0.5(x-50)^2+1100`

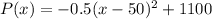
Therefore, the vertex (maximum point) of the profit function is (50, 1100).

This means that the maximum profit is $1,100 when the company produces 50 items.

As the company produces more units beyond the optimal level (50 items), the profit starts to decline. Therefore, producing 10 more units beyond the optimal level leads to increased costs exceeding the additional revenue gained, resulting in lower overall profit.