Question

Suppose that Nadine in Problem 1 has a production function

3x1+x2. If the factor prices are $3 for factor 1 and $3 for factor
2, how much will it cost her to produce 80 units of output?

Answer 1

To produce 80 units of output with a production function
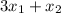`\(3x_1 + x_2\)`, and factor prices of $3 for both factors, the total cost for Nadine would be $240. This is calculated by substituting the output quantity into the cost function
`\(C = 3x_1 + 3x_2\)`.

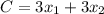Step-by-step explanation:

To determine Nadine's production cost for producing 80 units with the given production function
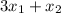`\(3x_1 + x_2\)`, where
`\(x_1\)` and
`\(x_2\)` are the quantities of factors 1 and 2, respectively, we incorporate the prices of the factors. With factor prices set at $3 for both factors, the cost function becomes
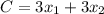`\(C = 3x_1 + 3x_2\)`. To find the specific quantities of factors needed for 80 units of output, we substitute this output level into the production function:
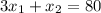`\(3x_1 + x_2 = 80\)`. Solving this equation yields the factor quantities required for the desired output.

With
`\(x_1\)` and
`\(x_2\)` determined, we then substitute these values into the cost function to compute the total cost of production. In this case, the total cost is $240
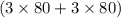`(\(3 * 80 + 3 * 80\))`. Thus, Nadine's cost to produce 80 units is $240, reflecting the combined impact of the production function and the prices of the factors of production. This analysis provides a comprehensive understanding of the cost structure associated with Nadine's production process, offering insights into the economic considerations involved in her production decisions.