Question

PLEASE HELP!!!

Find all zeros of ƒ(x) = x^2(x – 100)(x – 200). Then determine the multiplicity at each zero. State whether the graph will touch or cross the x-axis at the zero.
a. x = 0, multiplicity = 2, touch
x = 100, multiplicity = 1, cross
x = 200, multiplicity = 1, cross
b.x = 0, multiplicity = 2, touch
x = –100, multiplicity = 1, cross
x = –200, multiplicity = 1, cross
c .x = 0, multiplicity = 2, touch
x = –100, multiplicity = 1, cross
x = 200, multiplicity = 1, cross
d .x = 0, multiplicity = 2, cross
x = 100, multiplicity = 1, touch
x = 200, multiplicity = 1, touch

Answer 1

Answer: Choice A

x = 0, multiplicity = 2, touch

x = 100, multiplicity = 1, cross

x = 200, multiplicity = 1, cross

=============================================

Step-by-step explanation:

The zero product property will be used here.

It's the idea that if PQ = 0 then either P = 0 or Q = 0, or both.

This idea lets us set each factor equal to 0 to solve for x.

• x^2 = 0 leads to x = 0
• x-100 = 0 leads to x = 100
• x-200 = 0 leads to x = 200

The first equation x^2 = 0 appears to solve to one solution, but the reality is that solution is repeated twice. This is because of the exponent 2. This is the multiplicity. When the multiplicity is even, the curve will touch the x axis at one spot. It approaches the x axis, touches it, then bounces away like a tennis ball.

On the other hand, if the multiplicity is odd, then the curve will cross over the x axis.

These claims can be confirmed using a graphing tool like GeoGebra or Desmos.

Answer 2

a. x = 0, multiplicity = 2, touch

x = 100, multiplicity = 1, cross

x = 200, multiplicity = 1, cross

Step-by-step explanation:

In mathematics, a zero of a function is a value of the independent variable for which the function evaluates to zero.

The multiplicity of a zero is the exponent of the factor.

If the multiplicity is odd, the graph will cross the x-axis.

If the multiplicity is even, the graph will touch the x-axis.

To find the zeros of the given factored function f(x) = x²(x - 100)(x - 200), set each factor equal to zero, and solve for x.

To find the multiplicities of each zero, observe the exponent of each factor.

Factor 1

`x^2 = 0\implies \boxed{x=0}`

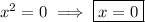
This factor has a zero at x = 0.

The multiplicity at this zero is 2 because of the factor is quadratic. The graph will touch the x-axis at this zero.

Factor 2

`x - 100 = 0 \implies \boxed{x=100}`

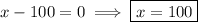
This factor has a zero at x = 100.

The multiplicity at this zero is 1 because the factor is linear. The graph will cross the x-axis at this zero.

Factor 3

`x - 200 = 0 \implies \boxed{x=200}`

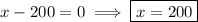
This factor has a zero at x = 200.

The multiplicity at this zero is 1 because the factor is linear. The graph will cross the x-axis at this zero.

In summary

• x = 0, multiplicity = 2, touch
• x = 100, multiplicity = 1, cross
• x = 200, multiplicity = 1, cross