Question

Convert θ = 3π /4 to rectangular form.

Answer 1

`x=r\cos\left( (3\pi )/(4)\right)\implies x=(1)\left( -\cfrac{1}{√(2)} \right)\implies x=-\cfrac{1}{√(2)} \\\\\\ y=r\sin\left( (3\pi )/(4)\right)\implies y=(1)\left( \cfrac{1}{√(2)} \right)\implies y=\cfrac{1}{√(2)}`

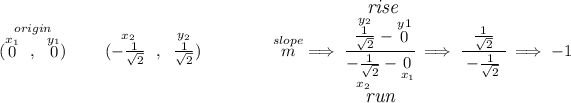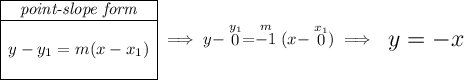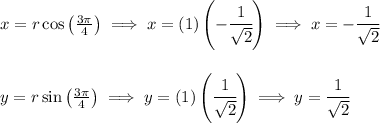
so over the Unitary circle, with a radius of 1 or namely a modulus of 1, we have a point with those coordinates above, and since the angle θ is a central angle, we can also say the line that touches those coordinates above also touches the origin, now, let's get its slope and thus its rectangular equation.

`\stackrel{ origin }{(\stackrel{x_1}{0}~,~\stackrel{y_1}{0})}\qquad (\stackrel{x_2}{-(1)/(√(2))}~,~\stackrel{y_2}{(1)/(√(2))}) ~\hfill~ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{(1)/(√(2))}-\stackrel{y1}{0}}}{\underset{\textit{\large run}} {\underset{x_2}{-(1)/(√(2))}-\underset{x_1}{0}}} \implies \cfrac{ ~~ (1)/(√(2)) ~~ }{-(1)/(√(2))} \implies -1`

`\begin{array} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{0}=\stackrel{m}{-1}(x-\stackrel{x_1}{0})\implies {\Large \begin{array}{llll} y=-x \end{array}}`