Question

a weight lifter maximum amount he can lift is 300 pound. Write and solve an inequality to find the number of 50-pound wights he can possibly lift

Answer 1

300 ≥ 50x

300/50=6

x = 6

He can lift 6, 50-pound weights.

Explanation:

Answer 2

He possibly lifts maximum 6 fifty-pound weights.

Explanation:

Let's assume the number of 50-pound weights the weight lifter can lift is represented by x.

The total weight the weightlifter can lift is the product of the number of 50-pound weights (x)

and

the weight of each 50-pound weight (50 pounds).

So, the inequality to find the number of 50-pound weights he can possibly lift is:

`\sf 50x \leq 300`

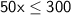
Now, let's solve the inequality for x:

Divide both sides by 50 to isolate x:

`\sf x \leq (300 )/(50)`

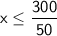
x ≤ 6

Therefore, the weight lifter can possibly lift a maximum of 6 fifty-pound weights.