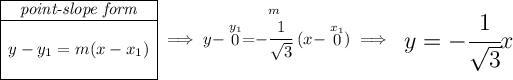Question

Convert 6cis 5π/6 to rectangular form.

Answer 1

`6\left[ \cos\left( (5\pi )/(6) \right)+i\sin\left( (5\pi )/(6) \right) \right]\implies 6\left[ -\cfrac{√(3)}{2}+i\cfrac{1}{2} \right]\implies -3√(3)+3i\implies (-3√(3),3)`

so we know the rectangular line will have a point at those coordinates above and since it has a central angle stemming from the center, it also passes through the origin, so let's use those two points to get our slope and thus its rectangular equation or namely its linear equation.

`\stackrel{ origin }{(\stackrel{x_1}{0}~,~\stackrel{y_1}{0})}\qquad (\stackrel{x_2}{-3√(3)}~,~\stackrel{y_2}{3}) ~\hfill~ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{3}-\stackrel{y1}{0}}}{\underset{\textit{\large run}} {\underset{x_2}{-3√(3)}-\underset{x_1}{0}}} \implies -\cfrac{1}{√(3)}`

`\begin{array} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{0}=\stackrel{m}{-\cfrac{1}{√(3)}}(x-\stackrel{x_1}{0})\implies {\Large \begin{array}{llll} y=-\cfrac{1}{√(3)}x \end{array}}`