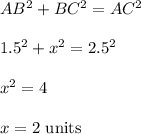Question

Determine the value of x. An image of a circle. A segment tangent to the circle is drawn. A radius is drawn to the tangent segment. A final segment is drawn connecting the center of the circle to the endpoint of the tangent segment. The length of the tangent segment is labeled x. The segment from the center of the circle to the endpoint of the tangent segment is divided into a segment that lies on the interior of the circle and a segment that lies on the exterior of the circle. The length of the segment on the interior of the circle has a length of 1.5 units. The length of the segment that lies on the exterior of the circle is 1 unit. Question 1 options: x = 1 x = 2.5 x = 2.9 x = 2

Answer 1

2 units

Explanation:

(Please see thet attached digram for more info)

As the angle between a tangent and a radius is 90 degrees, we know that ΔABC is right-angled at B. The interior segment is equal to the radius (AB) which is 1.5, and if the exterior segment is 1, then we know that the tota length of the segment, AC, = 2.5 units.

Now using pythagoras,

`AB^(2) + BC^(2) = AC^(2) \\\\1.5^(2) + x^(2) = 2.5^(2)\\\\x^(2) = 4 \\\\x = 2 \ \text{units}`