Question

A car is travelling with a constant velocity of 36 km h-¹. The driver sees a cow on the road at a distance 28 m from the current position. If the car decelerates at 2 m s², will the car hit the cow?​

Answer 1

No, the vehicle will stop in
`25\; {\rm m}`.

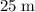Step-by-step explanation:

To determine if the vehicle will hit the cow, make use of the SUVAT equations to find the additional distance travelled before the vehicle stops completely. If the distance required for the vehicle to stop is less than the initial distance between the cow and the vehicle, the vehicle will not hit the cow.

Start by ensuring that all quantities are measured in standard units. Specifically, velocity should be measured in meters per second. The initial velocity of the vehicle would be equal to:

`\begin{aligned}u &= 36\; {\rm km \cdot h^(-1)} * \frac{1\; {\rm h}}{3600\; {\rm s}} * \frac{1000\; {\rm m}}{1\; {\rm km}} \\ &= 10\; {\rm m\cdot s^(-1)}\end{aligned}`.

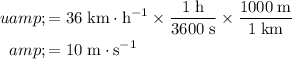In this scenario, the following quantities are known:

• Initial velocity
  `u = 36\; {\rm km\cdot h^(-1)} = 10\; {\rm m\cdot s^(-1)}`,
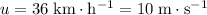• Final velocity
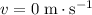  `v = 0\; {\rm m \cdot s^(-1)}`, since the vehicle would have stopped completely, and
• Acceleration
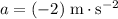  `a = (-2)\; {\rm m\cdot s^(-2)}`, which is negative since the vehicle is slowing down.

The quantity that needs to be found is the displacement
`x` of the vehicle during the time required for its velocity to change from
`u = 10\; {\rm m\cdot s^(-1)}` to
`v = 0\; {\rm m\cdot s^(-1)}` at the given rate of
`a = (-2)\; {\rm m\cdot s^(-2)}`.

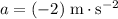Apply the SUVAT equation that relates
`u`,
`v`,
`a`, and
`x` to find the value of
`x\!`:

`v^(2) - u^(2) = 2\, a\, x`.

`\begin{aligned}x &= (v^(2) - u^(2))/(2\, a) \\ &= (0^(2) - 10^(2))/(2\, (-2))\; {\rm m} \\ &= 25\; {\rm m}\end{aligned}`.

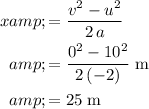In other words, the vehicle would stop completely within
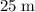`25\; {\rm m}`, which is
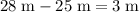`28\; {\rm m} - 25\; {\rm m} = 3\; {\rm m}` away from the cow. Hence, the vehicle will not hit the cow.