Question

Noah is baking a two-layer cake, in which the bottom layer is a circle and the top layer is a triangle. If segment AB = 5 inches and arc AB ≅ arc AC, what does Noah know about the top layer of his cake?

Circumscribed circle D around triangle ABC, arcs AB and AC are congruent.


A: segment AB is twice the length of segment BC because their arcs are congruent; therefore, ΔABC is an isosceles triangle.
B: segment AB is twice the length of segment BC because their arcs are congruent; therefore, ΔABC is an equilateral triangle.
C: segment AB ≅ segment BC because their arcs are congruent; therefore, ΔABC is an isosceles triangle.
D: segment AB ≅ segment BC because their arcs are congruent; therefore, ΔABC is an equilateral triangle.

Answer 1

C: segment AB ≅ segment BC because their arcs are congruent; therefore, ΔABC is an isosceles triangle.

Explanation:

Given:

• 
  `\sf \overline{\sf AB} = 5 \:inches`
• 
  `\sf \widehat{AB} \cong \widehat{AC}`
• Circumscribed circle D around triangle ABC

To find:

• Top layer of his cake = ?

Solution:

If arc AB and arc AC are congruent.

m ∡ACB ≅ m ∡ABC

Since the inscribed angle with the equal arcs are congruent and their segment are also congruent.

It's means:

`\sf \overline{\sf AB} = \overline{\sf AC} =5 \:inches`

Δ ABC is an isosceles triangle. This is because two of the sides of the triangle are congruent.

Therefore, Answer is C:

segment AB ≅ segment BC because their arcs are congruent; therefore, ΔABC is an isosceles triangle.

The other option are incorrect. Let's see;

• Option A is incorrect because it states that AB is twice the length of BC. This is not necessarily true, as the arcs AB and AC could be congruent even if AB is not twice the length of BC.
• Option B is incorrect because it states that ΔABC is an equilateral triangle. This is not necessarily true, as an equilateral triangle has three sides of equal length, and we only know that two of the sides of ΔABC are equal.
• Option D is incorrect because it states that ΔABC is an equilateral triangle. This is not necessarily true, as an equilateral triangle has three angles of equal measure, and we only know that two of the angles of ΔABC are equal.

`\boxed{\green{\textsf{Happy To Help You !!!}}}`

Answer 2

C)
`\sf \overline{AB} \cong \overline{AC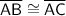}` because their arcs are congruent; therefore, ΔABC is an isosceles triangle.

Explanation:

The given diagram shows a circumscribed circle around triangle ABC, where arcs AB and AC are congruent.

From observation of the given circle:

• Angle ACB is subtended by arc AB.
• Angle ABC is subtended by arc AC.

As arc AB ≅ arc AC, then m∠ACB ≅ m∠ABC.

In an isosceles triangle, two sides are equal in length, and the angles opposite those sides are congruent. In this case, segment AB is congruent to segment AC because of the congruent angles ∠ACB and ∠ABC.

Therefore, the top layer of Noah's cake (ΔABC) is an isosceles triangle, and segment AB is equal in length to segment AC.