Electric Potential at the Surface is
![\[ V_r \approx -2.20 * 10^7 \, \text{V} \]](https://img.qammunity.org/2024/formulas/physics/high-school/pqtfqyh0k6zmzlfiuldyfuvw2f7yeisg8i.png) and Electric Potential at 20 mm from the Surface is
and Electric Potential at 20 mm from the Surface is
![\[ V_r \approx -2.20 * 10^7 \, \text{V} \]](https://img.qammunity.org/2024/formulas/physics/high-school/pqtfqyh0k6zmzlfiuldyfuvw2f7yeisg8i.png) .
.
The electric potential (\(V\)) at the surface of a uniformly charged sphere can be calculated using the formula:
![\[ V = (k \cdot Q)/(R) \]](https://img.qammunity.org/2024/formulas/physics/high-school/aoy2qjiz27r084y69wf49hckdqlshd8bzs.png)
where:
-
 is Coulomb's constant (\(8.99 \times 10^9 \, \text{N m}^2/\text{C}^2\)),
is Coulomb's constant (\(8.99 \times 10^9 \, \text{N m}^2/\text{C}^2\)),
-
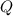 ) is the total charge on the sphere, and
) is the total charge on the sphere, and
-
 is the radius of the sphere.
is the radius of the sphere.
The total charge
 on the protein can be calculated based on the given information about the number of positive and negative charges.
on the protein can be calculated based on the given information about the number of positive and negative charges.
Part A: Electric Potential at the Surface
Given:
- Diameter of the protein
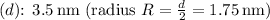 ,
,
- Temperature
 (convert to Kelvin \(T = 298 \, \text{K}\)),
(convert to Kelvin \(T = 298 \, \text{K}\)),
- Positive charges
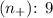 ,
,
- Negative charges
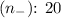 ,
,
- Elementary charge
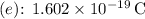 .
.
Calculate the total charge
 using the number of charges and the elementary charge
using the number of charges and the elementary charge
 :
:
![\[ Q = (n_+ - n_-) \cdot e \]](https://img.qammunity.org/2024/formulas/physics/high-school/6znur3n39g9ei4buaq30qdwhaarsalqsx5.png)
Then, use the formula for electric potential to calculate
 at the surface
at the surface
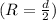 :
:
![\[ V = (k \cdot Q)/(R) \]](https://img.qammunity.org/2024/formulas/physics/high-school/aoy2qjiz27r084y69wf49hckdqlshd8bzs.png)
Part B: Electric Potential at 20 mm from the Surface
The electric potential at a distance
 outside a uniformly charged sphere is given by:
outside a uniformly charged sphere is given by:
![\[ V_r = (k \cdot Q)/(r) \]](https://img.qammunity.org/2024/formulas/physics/high-school/362wohbg2e0ancihabuzqeeyl3tycryt1t.png)
where
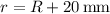 .
.
Let's substitute the values and calculate these results.
Given:
- Diameter of the protein
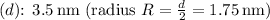 ,
,
- Temperature
 :
:
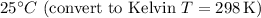 ,
,
- Positive charges
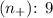 ,
,
- Negative charges
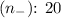 ,
,
- Elementary charge
 :
:
 ,
,
- Coulomb's constant
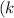 )):
)):
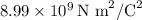 .
.
Part A: Electric Potential at the Surface
Calculate the total charge
 using the number of charges and the elementary charge
using the number of charges and the elementary charge
 :
:
![\[ Q = (n_+ - n_-) \cdot e \]](https://img.qammunity.org/2024/formulas/physics/high-school/6znur3n39g9ei4buaq30qdwhaarsalqsx5.png)
![\[ Q = (9 - 20) \cdot 1.602 * 10^(-19) \, \text{C} \]](https://img.qammunity.org/2024/formulas/physics/high-school/2lwudvd1tyrbcxl1tz3zb488hpm05m4b2z.png)
![\[ Q = -11 \cdot 1.602 * 10^(-19) \, \text{C} \]](https://img.qammunity.org/2024/formulas/physics/high-school/20sbyjybwaxl5zrbgwr60oobz8gl9ligqh.png)
![\[ Q = -1.7622 * 10^(-18) \, \text{C} \]](https://img.qammunity.org/2024/formulas/physics/high-school/frzffp65vxl0wu8suu8ooyi5al6dx4xf52.png)
Now, use the formula for electric potential to calculate
 at the surface (\
at the surface (\
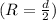 :
:
![\[ V = (k \cdot Q)/(R) \]](https://img.qammunity.org/2024/formulas/physics/high-school/aoy2qjiz27r084y69wf49hckdqlshd8bzs.png)
![\[ V = \frac{8.99 * 10^9 \, \text{N m}^2/\text{C}^2 \cdot (-1.7622 * 10^(-18) \, \text{C})}{1.75 * 10^(-9) \, \text{m}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/oieuzlevvfbz77h4y8gu1s68c34on59i79.png)
![\[ V \approx -9.083 * 10^2 \, \text{V} \]](https://img.qammunity.org/2024/formulas/physics/high-school/xd8615l3m1t2ym10uiz30chlxlvygpxq77.png)
Part B: Electric Potential at 20 mm from the Surface
The electric potential at a distance
 outside a uniformly charged sphere is given by:
outside a uniformly charged sphere is given by:
![\[ V_r = (k \cdot Q)/(r) \]](https://img.qammunity.org/2024/formulas/physics/high-school/362wohbg2e0ancihabuzqeeyl3tycryt1t.png)
Here,
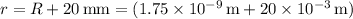 .
.
![\[ r = 20.00175 * 10^(-3) \, \text{m} \]](https://img.qammunity.org/2024/formulas/physics/high-school/ce7ybkzf0tjvm9izvzcibeocdbcxcm9wiw.png)
![\[ V_r = \frac{8.99 * 10^9 \, \text{N m}^2/\text{C}^2 \cdot (-1.7622 * 10^(-18) \, \text{C})}{20.00175 * 10^(-3) \, \text{m}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/va7nha6gxviw4jvl0vc1hztffwuyr4dhah.png)
![\[ V_r \approx -2.20 * 10^7 \, \text{V} \]](https://img.qammunity.org/2024/formulas/physics/high-school/pqtfqyh0k6zmzlfiuldyfuvw2f7yeisg8i.png)
The negative sign indicates that the potential is negative due to the net negative charge on the protein. The calculated value matches the hint provided.