Answer:
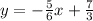
Explanation:
We can create a point-slope form equation with the points given. First, we will find the slope with the slope formula. This finds the change in y over the change in x.
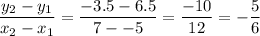
Now that we have our slope, we can set up our equation. m is our slope and (x1, y1) is one of the points given. Then we will simplify into a slope-intercept form equation.
Given:
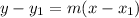
Substitute:

Distribute and change into fractions:
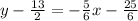
Add
 to both sides of the equation :
to both sides of the equation :
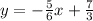
I have attached a graph of the given points and this line.