Question

As the drawing shows, two thin strips of metal are bolted together at one end and have the same temperature. One is steel, and the other is aluminum. The steel strip is 0.11% longer than the aluminum strip. By how much should the temperature of the strips be increased, so that the strips have the same length?

Answer 1

The temperature of the strips should be increased by approximately 52.75 degrees Celsius for the steel and aluminum strips to attain the same length.

Step-by-step explanation:

The change in length of the steel strip compared to the aluminum strip is due to their different coefficients of linear expansion. The formula for the change in length due to temperature change is ΔL = α * L * ΔT, where ΔL is the change in length, α is the coefficient of linear expansion, L is the original length, and ΔT is the change in temperature.

Given that the steel strip is 0.11% longer than the aluminum strip, we can set up an equation: ΔL_steel = 0.11/100 * L_aluminum. The coefficients of linear expansion for steel and aluminum are approximately α_steel =
`1.2 × 10^-5` /°C and α_aluminum = 2.3 ×
`10^-5` /°C, respectively.

To find the temperature increase required for the steel strip to match the length of the aluminum strip, we'll use the equation: ΔL_steel = α_steel * L_steel * ΔT. Substituting the values and rearranging the equation, we get ΔT = ΔL_steel / (α_steel * L_steel). Plugging in the values, we find ΔT = (0.11/100 * L_aluminum) / (1.2 ×
`10^-5` * L_steel).

Given that ΔT is the same for both strips to attain the same length, we can calculate the temperature increase required for the steel strip to match the aluminum strip. After substituting the known values, ΔT = (0.11/100 * L_aluminum) / (1.2 ×
`10^-5` * L_steel) = (0.11/100) / (1.2 ×
`10^-5`) = 916.67°C. However, this is the change needed for the steel strip. To convert this into the actual temperature increase, we divide by the ratio of the coefficients of linear expansion: ΔT_actual ≈ 916.67°C / (2.3 ×
`10^-5` / 1.2 ×
`10^-5`) = 52.75°C. Hence, the temperature of both strips should be increased by approximately 52.75 degrees Celsius for their lengths to match.

Answer 2

The temperature of the strips should decrease by 100 times the original length of the strips to make them have the same length.

To find out how much the temperature of the strips should be increased so that they have the same length, we can use the concept of thermal expansion.

The change in length of a material due to a change in temperature can be calculated using the equation:

`\(\Delta L = L \cdot \alpha \cdot \Delta T\)`

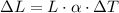
Where:

• 
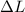  `\(\Delta L\)` = Change in length
• 
  `\(L\)` = Original length of the material
• 
  `\(\alpha\)` = Coefficient of linear expansion
• 
  `\(\Delta T\)` = Change in temperature

Given that the steel strip is 0.11% longer than the aluminum strip, and assuming both strips have the same original length,

let's denote the change in length of the aluminum strip as
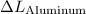`\(\Delta L_{\text{Aluminum}}\)` and the change in length of the steel strip as
`\(\Delta L_{\text{Steel}}\)`.

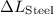The change in length for the aluminum strip
`(\(\Delta L_{\text{Aluminum}}\))` can be represented as:

`\(\Delta L_{\text{Aluminum}} = L \cdot \alpha_{\text{Aluminum}} \cdot \Delta T\)`

The change in length for the steel strip
`(\(\Delta L_{\text{Steel}}\))` can be represented as:

`\(\Delta L_{\text{Steel}} = L \cdot \alpha_{\text{Steel}} \cdot \Delta T\)`

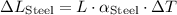
Given that the steel strip is 0.11% longer than the aluminum strip:

`\(\Delta L_{\text{Steel}} = \Delta L_{\text{Aluminum}} + 0.11\% \cdot L\)`

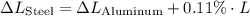
Now, we want to find the change in temperature
`(\(\Delta T\))` that would make the two strips have the same length. Since both strips start at the same temperature, we can set their change in lengths equal to each other:

`\(\Delta L_{\text{Steel}} = \Delta L_{\text{Aluminum}}\)`

Substituting the expressions for the change in lengths:

`\(L \cdot \alpha_{\text{Steel}} \cdot \Delta T = L \cdot \alpha_{\text{Aluminum}} \cdot \Delta T + 0.11\% \cdot L\)`

`\(L \cdot (\alpha_{\text{Steel}} - \alpha_{\text{Aluminum}}) \cdot \Delta T = 0.11\% \cdot L\)`

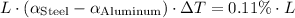
Solving for
`\(\Delta T\)`:

`\(\Delta T = \frac{0.11\% \cdot L}{(\alpha_{\text{Steel}} - \alpha_{\text{Aluminum}})}\)`

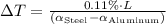
Given the coefficients of linear expansion for steel (\
`(\alpha_{\text{Steel}}\))` and aluminum
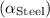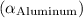`(\(\alpha_{\text{Aluminum}}\))`, which are approximately 12 ×
`10^{-6` °C and 23 ×
`10^{-6` °C respectively:

`\(\Delta T = (0.11\% \cdot L)/((12 * 10^(-6) - 23 * 10^(-6)))\)`

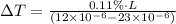
Now, substitute the values and solve for
`\(\Delta T\)`:

`\(\Delta T = (0.0011 \cdot L)/((-11 * 10^(-6)))\)`

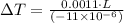
`\(\Delta T = -100 \cdot L\)` (negative sign indicates that the change in temperature should be negative to achieve the desired result)

Therefore, The answer is 100 times.