Question

Consider steady one-dimensional heat conduction in a large plane wall of thickness L and constant thermal conductivity k with no heat generation. Obtain expressions for the variation of temperature within the wall for the following pairs of boundary conditions (Fig. 2-43):

{ (a) }-k \frac{d T(0)}{d x}=\dot{q}_{0}=40 {~W} / {cm}^{2} { and } T(0)=T_{0}=15° {C}
{ (b) }-k \frac{d T(0)}{d x}=q_{0}=40 {~W} / {cm}^{2} { and } \quad-k \frac{d T(L)}{d x}=q_{L}=-25 {~W} / {cm}^{2}
(c) -k \frac{d T(0)}{d x}=\dot{q}_{0}=40 {~W} / {cm}^{2} and \quad-k \frac{d T(L)}{d x}=\dot{q}_{L}=\dot{q}_{0}=40 {~W} / {cm}^{2}

Answer 1

Consider steady one-dimensional heat conduction in a large plane wall of thickness L and constant thermal conductivity k with no heat generation. Obtain expressions for the variation of temperature within the wall for the following pairs of boundary conditions is.

`(a) \( T(x) = T_0 - \frac{\dot{q}_0}{2k}x^2 \)`

`(b)\( T(x) = T_0 - (q_0)/(2k)x + (q_L)/(2k) \left( L - x \right) \)`

`(c) \( T(x) = T_0 - \frac{\dot{q}_0}{2k}x^2 + \frac{\dot{q}_0}{2kL}x \left( L - x \right) \)`

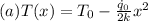
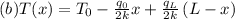
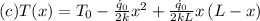
Step-by-step explanation:

In the given problem of one-dimensional heat conduction through a plane wall with constant thermal conductivity k we derive the temperature distribution for different boundary conditions.

`(a)For the first case where \( -k (dT(0))/(dx) = \dot{q}_0 = 40 \ W/{cm}^2 \) and \( T(0) = T_0 = 15^\circ C \) the solution is \( T(x) = T_0 - \frac{\dot{q}_0}{2k}x^2 \).`

`(b) In the second case with \( -k (dT(0))/(dx) = q_0 = 40 \, W/{cm}^2 \) and \( -k (dT(L))/(dx) = q_L = -25 \, W/{cm}^2 \) the temperature distribution is \( T(x) = T_0 - (q_0)/(2k)x + (q_L)/(2k) \left( L - x \right) \).`

`(c) For the third case, with \( -k (dT(0))/(dx) = \dot{q}_0 = 40 \ W/{cm}^2 \) and \( -k (dT(L))/(dx) = \dot{q}_L = \dot{q}_0 = 40 \ W/{cm}^2 the temperature variation is \( T(x) = T_0 - \frac{\dot{q}_0}{2k}x^2 + \frac{\dot{q}_0}{2kL}x \left( L - x \right) \).`

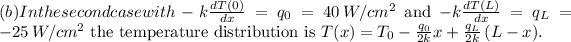
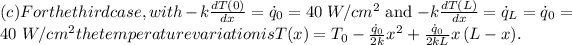
The solutions are obtained through steady-state heat conduction equations and appropriate boundary conditions providing insights into temperature profiles within the wall under different scenarios. The quadratic and linear terms in the solutions represent the balance between heat generation and heat dissipation across the wall.