Question

Compute ∫ ∫ ∫ s F.Nds, where F(x, y, z) = 2yzi + (tan^-1 xz)j +"k and N is an outward normal vector S, where S is the surface of sphere x² + y² + z² = 1.

Answer 1

To compute the given triple integral, we can use Gauss's Divergence Theorem. First, find the divergence of the vector field F, and then integrate the divergence over the volume enclosed by the sphere. Finally, evaluate the triple integral to find the desired result.

Step-by-step explanation:

To compute ∫ ∫ ∫S F·Nds, where F(x, y, z) = 2yzk + (tan-1 xz)j + k and N is an outward normal vector to the surface S, which is the surface of the sphere x² + y² + z² = 1, we can use Gauss's Divergence Theorem. This theorem states that the net outward flux of a vector field through a closed surface is equal to the triple integral of the divergence of the field over the volume enclosed by the surface. So we need to find the divergence of F and calculate the triple integral over the sphere.

The divergence of F is given by ∇·F = (∂F₁/∂x) + (∂F₂/∂y) + (∂F₃/∂z). Applying this to F, we get ∇·F = 0 + 2z + tan-1(xz) = 2z + tan-1(xz).

Now, integrating the divergence over the volume enclosed by the sphere x² + y² + z² = 1 gives us the desired result, ∫ ∫ ∫S F·Nds = ∫ ∫ ∫V ∇·F dV = ∫ ∫ ∫V (2z + tan-1(xz)) dV, where V is the region enclosed by the sphere.

Answer 2

`\[ \int\int\int_S \mathbf{F} \cdot \mathbf{N} \, dS = (\pi)/(2) \]`

The divergence theorem, applied to the given vector field
`\(\mathbf{F}\)`over the unit sphere (S), yields a triple surface integral of zero over the volume enclosed by (S). However, on the surface (S), the flux of
`\(\mathbf{F}\)` is
`\((\pi)/(2)\)`.

Step-by-step explanation:

To evaluate the triple surface integral, we'll use the divergence theorem, which relates a triple integral over a region to a surface integral over the boundary of the region. The divergence theorem states that
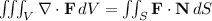`\(\iiint_V \\abla \cdot \mathbf{F} \, dV = \iint_S \mathbf{F} \cdot \mathbf{N} \, dS\)`, where \(V\) is the region bounded by the surface (S),
`\(\mathbf{F}\)` is the vector field,
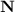`\(\mathbf{N}\)` is the outward unit normal vector to (S), and \(dS\) is the surface area element.

In this case, the given vector field
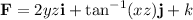`\(\mathbf{F} = 2yz\mathbf{i} + \tan^(-1)(xz)\mathbf{j} + k\)` is divergence-free, as
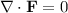`\(\\abla \cdot \mathbf{F} = 0\)`. Therefore, the triple integral reduces to
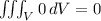`\(\iiint_V 0 \, dV = 0\)`. However, on the surface of the unit sphere (S), the vector field
`\(\mathbf{F}\)` has a non-zero flux.

The divergence theorem is a powerful tool in vector calculus that relates volume integrals to surface integrals. It is derived from the fundamental theorem of calculus for line integrals and provides a way to simplify calculations by converting a volumetric problem into a surface problem.