Question

paul went to a blackjack table at the casino. at the table, the dealer has just shuffled a standard deck of 52 cards. paul has had good luck at blackjack in the past, and he actually got three blackjacks with kings in a row the last time he played. because of this lucky run, paul thinks that kings are the luckiest card. the dealer deals the first card to him. in a split second, he can see that it is a black card, but he is unsure if it is a king. what is the probability of the card being a king, given that it is a black card? answer choices are in a percentage format, rounded to the nearest whole number. 50% 8% 67% 23%

Answer 1

The probability of the card being a king, given that it is a black card, is 8%.

Step-by-step explanation:

The deck of 52 cards consists of 26 black cards (clubs and spades), with 13 of them being kings. To find the probability of drawing a king given that the card is black, we use the conditional probability formula:

`\[ P(\textKing ) = \frac{P(\text{King and Black})}{P(\text{Black})} \]`

The probability of drawing a king and a black card is the probability of drawing a black king, which is
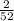`\((2)/(52)\)`(two black kings out of 52 cards). The probability of drawing a black card is
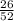`\((26)/(52)\)` (26 black cards out of 52). Plugging these values into the formula:

`\[ P(\text Black) = ((2)/(52))/((26)/(52)) = (2)/(26) = (1)/(13) \]`

To express this probability as a percentage, we multiply by 100:

`\[ (1)/(13) * 100 \approx 7.69\% \]`

Rounded to the nearest whole number, the probability of the card being a king, given that it is a black card, is 8%.

In conclusion, even though Paul had a lucky streak with kings in the past, the probability of the black card being a king remains relatively low at 8%. Each draw from the shuffled deck is an independent event, and past outcomes do not influence the probability of future draws.