Question

It says infinite solutions which means that the last number should also be a equal but its not so how do you solve it?

Answer 1

`(a)/(b) = (1)/(4)`

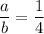
Step-by-step explanation:

To find the value of "a/b" when the system of equations has infinitely many solutions, we need to first determine the relationship between the two given equations. When two equations represent the same line or are scalar multiples of each other, they have infinitely many solutions, and the system is considered dependent.

Let's examine the given system of equations:

`\left\{\begin{array}{ccc}ax+by=12\\2x+8y=60\end{array}\right`

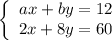
To see if these equations are scalar multiples of each other, we'll try to manipulate one equation to get it in the form of the other equation:

Let's multiply the first equation by a factor of 5:

`\Longrightarrow ax+by=12\\\\\\\\\Longrightarrow 5 \cdot\big[ax+by=12\big]\\\\\\\\\Longrightarrow \boxed{5ax+5by=60}`

Now, we can see that the second equation is already quite similar. Let's compare our new equation to equation (2):

`\Longrightarrow 5ax +5by = 2x + 8y`

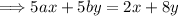
Comparing the 'x' term:

`\Longrightarrow 5a = 2\\\\\\\\\Longrightarrow \boxed{a = (2)/(5)}`

Comparing the 'y' term:

`\Longrightarrow 5b = 8\\\\\\\\\Longrightarrow \boxed{b = (8)/(5)}`

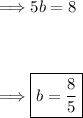
Thus,

`\Longrightarrow (a)/(b) = (\Big((2)/(5) \Big))/(\Big((8)/(5)\Big)) = (2)/(5) \cdot (5)/(8) = (2)/(8) = \boxed{(1)/(4)}\\\\\\\\\therefore \boxed{\boxed{(a)/(b) = (1)/(4) }}`

Therefore, the correct value of "a/b" is 1/4.

`\hrulefill`

Additional Information:

System of Equations: A set of two or more equations with the same variables.

Infinitely Many Solutions: When two or more equations in a system represent the same line or are scalar multiples of each other, the system has infinitely many solutions. Geometrically, the equations represent the same line, and all the points on that line satisfy both equations.

Dependent System: A system of equations with infinitely many solutions is called dependent. The equations are not independent and provide no unique solution.

Scalar Multiplication: When you multiply both sides of an equation by a constant (non-zero), you are performing scalar multiplication. This process does not change the solutions of the equation but can simplify the equation or make it easier to work with.

Coefficients: In a linear equation, the coefficients are the constants multiplying the variables. In the equations above, "a" and "b" are the coefficients of the variables "x" and "y," respectively.