Question

HELP ME PLS 100 POINTS

Answer 1

(1, 3, 2), follow the steps carefully to fill in the appropriate boxes.

Explanation:

Solve the given system of equations.

Given system:

`\left\{\begin{array}{ccc}x+y+z =6 \ (1)\\x-2y+3z =1 \ (2)\\x+3y-z=8 \ (3)\end{array}\right`

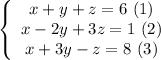
Eliminating "x":

Subtracting equation (2) from equation (1) to give us equation (4):

`\Longrightarrow \big[x+y+z=6\big] - \big[x-2y+3z=1\big]\\\\\\\\\Longrightarrow (x-x)+(y-(-2y))+(z-3z)=6-1\\\\\\\\\Longrightarrow (0)+(y+2y)+(-2z)=5\\\\\\\\\therefore \boxed{3y-2z=5} \ (4)`

Subtracting equation (3) from equation (1) to give us equation (5):

`\Longrightarrow \big[x+y+z=6\big] - \big[x+3y-z=8\big]\\\\\\\\\Longrightarrow (x-x)+(y-3y)+(z-(-z))=6-8\\\\\\\\\Longrightarrow (0)+(-2y)+(z+z)=-2\\\\\\\\\therefore \boxed{-2y+2z=-2} \ (5)`

Now adding equations (4) and (5) together, this will eliminate "z":


`\Longrightarrow \big[ 3y-2z=5\big]+\big[ -2y+2z=-2 \big]\\\\\\\\\Longrightarrow (3y+(-2y))+(-2z+2z)= 5+ (-2)\\\\\\\\\Longrightarrow (3y-2y)+(-2z+2z)= 5-2\\\\\\\\\Longrightarrow (y)+(0)= 3\\\\\\\\\therefore \boxed{y = 3}`

Substituting y = 3 into equation (4) and solving for "z":

`\Longrightarrow 3(3)-2z=5\\\\\\\\\Longrightarrow 9-2z=5\\\\\\\\\Longrightarrow 2z+5=9\\\\\\\\\Longrightarrow 2z=9-5\\\\\\\\\Longrightarrow 2z=4\\\\\\\\\therefore \boxed{z=2}`

Now taking y = 3 and z = 4 and substituting them into equation (1) to solve for "x":

`\Longrightarrow x+3+2=6\\\\\\\\\Longrightarrow x+5=6\\\\\\\\\Longrightarrow x=6-5\\\\\\\\ \therefore \boxed{x=1}`

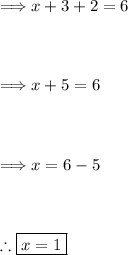
Thus, the solution to the given system of equations is (1, 3, 2).

`\hrulefill`

Terminology:

System of Equations: A system of equations is a collection of two or more equations that share common variables and are considered together as a unit. The goal of solving a system of equations is to find the values of the variables that satisfy all the given equations simultaneously. These solutions represent the points where the corresponding graphs of the equations intersect in a coordinate plane.

Solving a System using Elimination: Solving a system of equations using elimination involves eliminating one variable by adding or subtracting the equations in the system. The goal is to manipulate the equations in a way that results in the elimination of one variable, thus reducing the system to a single equation with only one variable. This process is then repeated until all variables are eliminated, and the final solution is obtained by back-substituting the found values into the original equations.

Solving a System using Substitution: Solving a system of equations using substitution involves isolating one variable in one of the equations and then substituting its value into the other equations. This process is repeated until the remaining variable can be easily solved. The final solutions represent the values of the variables that satisfy all the equations in the system simultaneously.