Answer:
3x-4y=-40
Explanation:
Hi there!
We're given the equation of the line, y-4=3/4(x+8) in point-slope form (y-
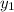 =m(x-
=m(x-
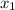 ), where (
), where (
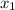 ,
,
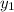 ) is a point and m is the slope)
) is a point and m is the slope)
We need to convert y-4=3/4(x+8) into standard form (ax+by=c, where a, b, and c are integer coefficients; a CANNOT be 0, and CANNOT be negative).
So we need to get y-4=3/4(x+8) out of point-slope form
We can do this by converting the equation into slope-intercept form, which is y=mx+b, where m is the slope and b is the y intercept
to do this, we need to isolate y by itself in the equation
first, do the distributive property and distribute 3/4 on the right side
y-4=3/4x+6
add 4 to both sides
y=3/4x+10
now the equation is in slope-intercept form, but remember, we want it in standard form
x and y are on the same side in standard form, so let's subtract 3/4 x from both sides
-3/4x+y=10
however we aren't done; in standard form, the coefficients need to be integers (whole numbers), and a (the coefficient in front of x) CANNOT be negative
so let's multiply both sides by -4 to clear the fraction and change the sign of a
-4(-3/4x+y)=-4(10)
do the distributive property
3x-4y=-40
Hope this helps! :)