Answer:
Approximately
 from the
from the
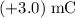 charge, which is approximately
charge, which is approximately
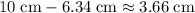 from the
from the
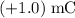 charge.
charge.
Step-by-step explanation:
To find the position of the charge, start by determining the position of this new charge relative to the two fixed charges- between the two charges, or on the same side of the two charges. After that, apply Coulomb's Law to find the magnitude of the force from each fixed charge. Set the two magnitudes to be equal and solve the equation to find the position of the required charge.
Forces from the two fixed charge would be balanced only if the two forces are in opposite directions. Assuming that the new charge is positive, it will repel both fixed charges:
- If the new charge is to the left of both fixed charges, forces from both fixed charge would point to the left (further away from the fixed charges.) Hence, the resultant force would be nonzero.
- If the new charge is to the right of both fixed charges, forces from both fixed charges would point to the right. The resultant force would also be nonzero.
- If the new charge is between the two fixed charges, the force from the fixed charge on the left would point to the right, while the force from the fixed charge on the right would point to the left. The resultant force could be balanced since the two forces point in opposite directions.
Similarly, it can be shown that if the new charge is negative, the force from the two fixed charges would be balanced only if the new charge is between the two fixed charges.
Assume that the new charge is between the two fixed charges and is at a distance of
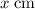 from the
from the
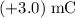 charge (
charge (
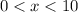 .)
.)
Since the
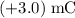 fixed charge is at a distance of
fixed charge is at a distance of
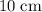 from the
from the
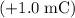 fixed charge, the distance between the new charge and the
fixed charge, the distance between the new charge and the
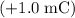 fixed charge would be
fixed charge would be
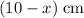 .
.
By Coulomb's Law, when two charges of magnitude
 and
and
 are at a distance of
are at a distance of
 from each other, the magnitude of the electrostatic force between them would be:
from each other, the magnitude of the electrostatic force between them would be:
 ,
,
Where
 is the coulomb constant.
is the coulomb constant.
Let
 denote the magnitude of the new charge. Magnitude of the force between the new charge and the
denote the magnitude of the new charge. Magnitude of the force between the new charge and the
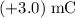 charge would be:
charge would be:
 .
.
Magnitude of the force between the new charge and the
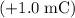 charge would be:
charge would be:
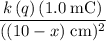 .
.
Equate the two expressions and solve for
 :
:
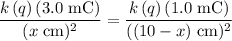 .
.
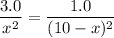 .
.
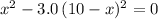 .
.
The two real roots of this quadratic equation are
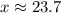 and
and
 . Since the new charge needs to be located between the two fixed charges,
. Since the new charge needs to be located between the two fixed charges,
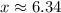 is the only valid solution.
is the only valid solution.
Therefore, the new charge should be approximately
 from the
from the
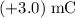 charge, which is approximately
charge, which is approximately
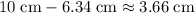 from the
from the
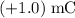 charge.
charge.