Question

Write whether the following statements are true or false. justify your answer

(I) Area of triangle ABC is 8cm^2 in which AB = AC = 4cm and angle A = 90°
(ii) The area of the equilateral triangle is 20√3cm^2 whose side is 8 cm
(iii) The area of the isosceles triangle is 5/4√11cm^2, if the perimeter is 11cm and the base is 5cm​

Answer 1

True, False, True

Explanation:

(i) Using the formula 1/2bh, we get that

`A = (1)/(2)(4)(4) = 8\text{cm}^(2)`

So (i) is true

(ii) All three angles in an equilateral triangle are 60°, so using the formula 1/2absinC,

`A = (1)/(2)(8)(8)(\text{sin}60) = 32((√(3))/(2)) = 16√(3)\text{cm}^(2)`

Hence (ii) is false

(iii) Subtracting 5 from the perimeter and dividng by 2, we get that the 2 equal lengths of the iscosceles triangle are equal to 3cm. To get the the area we first draw a perpendicular line from the top of the triangle which bisects the base, allowing us to use pythagoras to get the height of the triangle:

`h^(2) = 3^(2) - ((5)/(2))^(2) = (11)/(4) \\\\ h = (√(11))/(2)\text{cm}`

Now using the formula 1/2bh,

`A = (1)/(2)(5)((√(11))/(2)) = (5)/(4)√(11)\text{cm}^(2)`

Therefore (iii) is true

Answer 2

Heya There!

Question:

Write whether the following statements are true or false. justify your answer:

---------------------------------------------

(I) Area of triangle ABC is 8cm² in which AB=AC=4cm and angle A = 90°.

Solution:

The statement is true.

Step-by-step Explanation:

In ∆ABC, it is given that AB = AC = 4 cm and ∠A = 90°.

We know,

• Area of ∆ABC = ½(Base x Height)

= ½ (AB x AC )

= ½ (4 x 4)

= 8 cm²

It is given that area of ∆ABC is 8 cm². Hence, the given statement is true...

-------------------------------------------

(ii) The area of the equilateral triangle is 20√3cm² whose side is 8 cm.

Solution:

The statement is false.

Step-by-step Explanation:

The area of an equilateral triangle whose each side is 8 cm is given by,

• The Area of equilateral triangle is:

`= ( √(3) )/(4) ( {side)}^(2)`

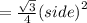
As given, side = 8cm

`= ( √( 3) )/(4) * {8}^(2) {cm}^(2)`

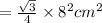
= 16√3 cm²

But, area of triangle is given as 20√3 cm². Hence, the given statement is false...

-------------------------------------------

(iii) The area of the isosceles triangle is 5/4√11cm² , if the perimeter is 11cm and the base is 5cm.

Solution:

The statement is true

Step-by-step Explanation:

Let the length of each equal side of isosceles triangle be x cm.

The length of the base be a cm.

we know, perimeter of the isosceles ∆:

• 2x + a , where a is side

It is given that,

Perimeter = 11cm , Base = 5 cm.

so, applying formula: we get

`= > x + x + a = 11`

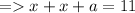
As given ( a = 5 ),

`= > 2x + 5 = 11`

`= > 2x = 11 - 5 = 6`

`= > x = (6)/(2) = 3`

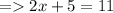
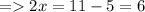
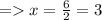
so , x = 3 and a = 5

Now, we know Area of triangle:

`= (1)/(2) a \sqrt{ {x}^(2) - \frac{ {a}^(2) }{4} }`

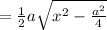
Putting given values, x = 3 , a = 5

`= (1)/(2) * 5 * \sqrt{ {3}^(2) - \frac{ {5}^(2) }{4} }`

`= (1)/(2) * 5 * \sqrt{9 - (25)/(4) }`

`= (1)/(2) * \sqrt{ (36 - 25)/(4) }`

`= (1)/(2) * 5 * \sqrt{ (11)/(4) }`

`= (1)/(2) * 5 * ( √(11) )/(2)`

`= (5)/(4) √(11) {cm}^(2)`

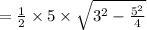
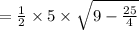
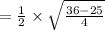
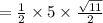
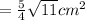
Also, it is given that area of triangle is 5/4√11cm². Hence, the given statement is true..

-------------------------------------------

Please see the attachment for better understanding ^_^...

Hope this helps you :)

#carryonlearning :)