Answer:
8 rows
Explanation:
We can think of the number of seats in each row as an arithmetic sequence, where the first term, a, = 12 and the common difference, d, = 2. So the sequence would be 12, 14, 16, ... k, and the row corresponds to the position of the term in the sequence. So the sum of n rows (terms) = 152.
Using the formula for sum of terms,

Now we solve for n as follows:
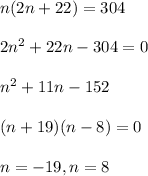
However we can't have a negative number of rows so we take 8 rows as our solution.