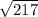Question

Question 8 of 10

What is the length of EF in the right triangle below?
D
19
ооо
12
□
F
A. 505
B. 217
C. √217
D. 22
E. √505
F. 7

Answer 1

Using the Pythagorean Theorem, we have:

`$19^(2)=b^(2)+12^(2)$`

`361=b^(2)+144`

`217=b^(2)`

`√(217)=b`

So, C)
`√(217)`, is our answer.

Answer 2

C

Explanation:

using Pythagoras' identity in the right triangle

the square on the hypotenuse is equal to the sum of the squares on the other 2 sides.

here hypotenuse is ED and the other sides are EF and DF , then

EF² + DF² = ED² ( substitute values )

EF² + 12² = 19²

EF² + 144 = 361 ( subtract 144 from both sides )

EF² = 217 ( take square root of both sides )

EF =
`√(217)`