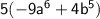Question

Find the complete factored form of the polynomial
-45a^6 + 20b^5

Answer 1

Complete factored form is
`\sf 5(-9a^6+4b^5)`

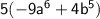
Explanation:

To find the complete factored form of the polynomial
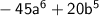`\sf -45a^6 + 20b^5`, we can factor out the common factors from both terms.

`\sf -45a^6 + 20b^5`

`\sf -3*3 *5*a^6 + 2*2*5*b^5`

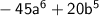
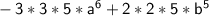
In this case, common factor is 5.

So,

Taking common and keeping remaining in bracket.

`\sf 5(-3*3*a^6+2*2*b^5)`

Expand

`\sf 5(-9a^6+4b^5)`

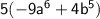
Therefore, complete factored form of the polynomial is
`\sf 5(-9a^6+4b^5)`