Answer:
Probability is
 or 37.5 %
or 37.5 %
Explanation:
To find the probability of exactly two heads in three fair coin tosses, we need to consider all the possible outcomes and count the favorable outcomes where we get exactly two heads.
Total possible outcomes when tossing three fair coins:
 Possible outcomes.
Possible outcomes.
(each coin can have two outcomes: heads or tails)
The favorable outcomes to get exactly two heads:
- HHT (Head, Head, Tail)
- HTH (Head, Tail, Head)
- THH (Tail, Head, Head)
So, there are 3 favorable outcomes.
Now,
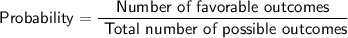
Substituting value

In Percentage

= 37.5 %
Therefore, the probability of exactly two heads in three fair coin tosses is
 or 37.5 %
or 37.5 %