Question

What is the value of y in 3^y+1 - 3^y = 54?​

Answer 1

Hi,

Explanation:

`3^(y+1)-3^y=54\\\\\Longleftrightarrow\ 3^y*(3-1)=54\\\\\\\Longleftrightarrow\ 3^y=(54)/(2) \\\\\Longleftrightarrow\ 3^y=27\\\\\Longleftrightarrow\ 3^y=3^3\\\\\boxed{y=3}`

Answer 2

y = 3

Explanation:

The given equation is:

`\sf 3^(y+1 )- 3^y = 54`

We can rewrite the left-hand side of the equation as follows:

`\sf 3^y*3- 3^y = 54`

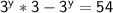
Taking common
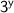`\sf 3^y` in left side

`\sf 3^y * (3 - 1) = 54`

`\sf 3^y * 2 = 54`

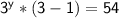
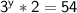
Dividing both sides of the equation by 2, we get:

`\sf (3^y*2)/(2)= (54)/(2)`

`\sf 3^y = 27`

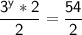
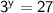
Since 27 is equal to
`3^3`

so,

`3^y = 3^3`

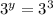
we can compare the power if it has same base.

While comparing, we get

y = 3

Therefore, the only integer value of y that satisfies this equation is y = 3.