Question

Solve the system of equations.
y=2x+2
y=3x^2+6x+1
Round to the nearest hundredth.

Answer 1

`\sf x \approx 0.22 \:\:and\:\: y \approx 2.44`

`\sf x \approx -1.55 \:\: and\:\: \approx -1.10`

Explanation:

Given system of equations:

1. y = 2x + 2

2. y = 3x^2 + 6x + 1

To find the solutions, set the expressions for y equal to each other:

`\sf 2x + 2 = 3x^2 + 6x + 1`

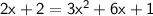
Rearrange to set it to zero:

`\sf 3x^2 + 6x - 2x + 1 - 2 = 0`

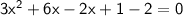
Simplify:

`\sf 3x^2 + 4x - 1 = 0`

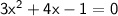
Now, use the quadratic formula:

`\sf x =\frac{ -b \pm √(b^2 - 4ac)} {2a}`

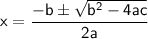
where a = 3, b = 4, and c = -1.

`\sf x=(-(4) \pm √((4)^2 - 4 * 3 * (-1)))/( 2 * 3)`

`\sf x = (-4 \pm √(28))/( 6)`

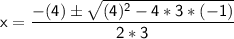
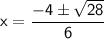
Now, calculate the two possible values of x:

`\sf x = (-4 + √(28))/( 6) \approx0.22`

`\sf x = (-4 - √(28))/( 6) \approx -1.55`

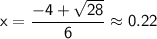
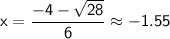
Now, find the corresponding values of y using the first equation:

`\sf For\: x \approx 0.22 :`

`\sf y = 2(0.22) + 2 \approx 2.44`

`\sf For \;\: x \approx -1.55:`

`\sf y = 2(-1.55) + 2 \approx -1.10`

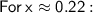
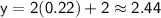
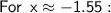
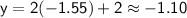
Thus, the solutions to the system of equations (rounded to the nearest hundredth) are:

`\sf x \approx 0.22 \:\:and\:\: y \approx 2.44`

`\sf x \approx -1.55 \:\: and\:\: \approx -1.10`