Question

For the function f(x) = sqrt(8x + 10) find the inverse function as well as the restricted domain.

Answer 1

See below

Explanation:

To find the inverse we can swap the x’s for y’s to get

`x = √(8y + 10)`

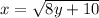
Now rearranging for y,

`x^(2) = 8y + 10\\\\8y = x^(2) - 10\\\\f^(-1)(x) = (x^(2) - 10)/(8)`

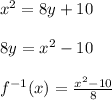
The domain of an inverse function is equal to the range of the original function. For f(x) the range is ≥ 0 as it is a square root function, hence the domain of the inverse is x ≥ 0.

(The pic I attached shows the two functions together)