Question

Monopoly: End of Chapter Yroblem Consider this situation for a monopolist. - Demand: P=100−2Q - Fixed cost =100 - Marginal cost =10 a. Use the information to calculate the variables indicated. i. The marginal revenue curve: MR= ii. The level of output where MR=MC:Q ∗ = iii. The profit-maximizing price: P ∗ =$ iv. Total revenue at Q ∗ :TR=$ Total cost at Q ∗ :TC=$ v. What entrepreneurs really care about-profit: $ iii. The profit-maximizing price: P ∗ =$ iv. Total revenue at Q ∗ :TR=$ Total cost at Q ∗ :TC=$ v. What entrepreneurs really care about-profit: $ b. Calculate markup, price minus marginal cost: $ Calculate markup as a percentage, 100× P−MC/MC ​ . Percentage markup:

Answer 1

The marginal revenue curve is MR = 100 - 4Q. The profit-maximizing quantity is 22.5 units at a price of $55, with a total revenue of $1237.5, total cost of $325, and a profit of $912.5. Markup is $45 with a percentage markup of 450%.

Step-by-step explanation:

Calculating Monopoly Profit-Maximization

To find the marginal revenue (MR) curve for a monopolist with the demand equation P=100−2Q, we first derive Total Revenue (TR), which is P×Q, resulting in TR=100Q−
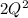`2Q^2`. The MR is the derivative of TR with respect to Q, which gives us MR=100−4Q.

Next, we set MR equal to the marginal cost (MC) to find the profit-maximizing level of output (Q*). Given the MC is constant at 10, we have 100−4Q = 10, solving for Q gives us Q* = (100−10)/4 = 22.5 units.

The profit-maximizing price (P*) is found by substituting Q* into the demand equation: P* = 100 - 2×22.5 = 55. Thus, P* = $55

Total revenue (TR) at Q* is TR = P×Q = 55×22.5 = $1237.5. Next, we calculate the total cost (TC) at Q* by adding fixed cost to variable cost, which is TC = 100 + (10×22.5) = $325. Therefore, TC = $325.

Profit is then the difference between total revenue and total cost, which is Profit = TR - TC = $1237.5 - $325 = $912.5.

To find the markup and percentage markup, we subtract the MC from the price: Markup = P - MC = 55 - 10 = $45, and the percentage markup is (45/10)×100 = 450%.