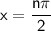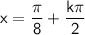Question

PLS HELP! 50 POINTS
Solve for x:
cos(x)*sin(7x)=cos(3x)*sin(5x)

Answer 1

`\sf x = (n\pi )/(2)`

`\sf x = (\pi)/(8 )+ (k\pi)/(2)`

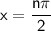
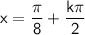
Explanation:

To solve the equation
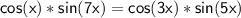`\sf cos(x)*sin(7x) = cos(3x)*sin(5x)` for x, we can use trigonometric identities. One useful identity here is the product-to-sum identity:

`\sf cos(A)*sin(B) = (1)/(2) [sin(A + B) + sin(A - B)]`

Let's apply this identity to the given equation:

cos(x) * sin(7x) = cos(3x) * sin(5x)

`\sf (1)/(2) * [sin(x + 7x) + sin(x - 7x)] = (1)/(2)* [sin(3x + 5x) + sin(3x - 5x)]`

Now, we can cancel out the common terms on both sides:

`\sf sin(8x) +sin(-6x) = sin(8x) - sin(-2x)`

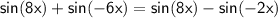
since
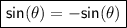`\boxed{\sf sin(\theta) = -sin(\theta)}`, the equation becomes:

`\sf sin(8x) - sin(6x) = sin(8x) - sin(2x)`

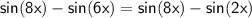
Next, move the terms involving sin(8x) to one side:

sin(8x) - sin(8x) = sin(2x) - sin(6x)

The left side simplifies to zero:

0 = sin(2x) - sin(6x)

Now, use another trigonometric identity:

`\boxed{\sf sin(A) - sin(B) = 2 * cos\left[((A + B))/(2)\right] * sin\left[((A - B))/(2)\right]}`

In this case, A = 6x and B = 2x:

`\sf 2 * cos\left[((6x + 2x))/(2)\right] * sin\left[((6x - 2x))/(2)\right] = 0`

Simplify further:

`\sf 2 * cos(4x) * sin(2x) = 0`

`\sf cos(4x) * sin(2x) = 0`

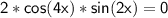
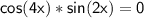
Now, there are two possibilities for this equation to hold true:

• cos(4x) = 0
• sin(2x) = 0

Let's solve each possibility:

cos(4x) = 0

`\sf 4x = cos^(-1)( 0)`

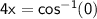
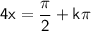`\sf 4x = (\pi)/(2) + k\pi`, where k is an integer

Solving for x

`\sf x = (\pi)/(8 )+ (k\pi)/(2)`

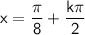
For sin(2x) = 0

In trigonometry, sin(θ) = 0 when θ is an integer multiple of π.

So for our equation, we have:

2x = nπ

where n is an integer.

Solving for x:

`\sf x = (n\pi )/(2)`

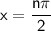
Therefore, Value of x are:

`\sf x = (n\pi )/(2)`

`\sf x = (\pi)/(8 )+ (k\pi)/(2)`