Question

solve the unknown for the following equations 1) 2(x+3)=x+1 2) 3(x-3)=2(x-2) 3) 4/3= x+3/4 4) 10x+5(x+5)

Answer 1

Answer: 1) x=
`-1(2)/(3)`

2) x=5

3) x=3/4

4) 15x+25

Explanation:

1) 2(x+3)=x+1

2x+6=x+1

2x+x=1-6

3x=-5

x=
`-1(2)/(3)`

2) 3(x-3)=2(x-2)

3x-9=2x-4

3x-2x=-4+9

x=5

3) 4/3= x+3/4

4=3(x+3/4)

4=3x+9/4

3x=4-9/4

3x=9/4

12x=9

x=3/4

4) 10x+5(x+5)

10x+5x+25

15x+25

Answer 2

1. x = -5

2. x = 5

3.
`\sf x =(7)/(12)`

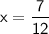
4. No solution

Explanation:

Let's solve the unknown (x) for each equation:

1) 2(x + 3) = x + 1

Expand the equation:

2x + 6 = x + 1

Subtract x from both sides:

2x - x + 6 = x - x + 1

Simplify:

x + 6 = 1

Subtract 6 from both sides:

x + 6 - 6 = 1 - 6

Simplify: x = -5

So, the solution for the 2(x + 3) = x + 1 is x = -5.

`\hrulefill`

2) 3(x - 3) = 2(x - 2)

Expand the equation:

3x - 9 = 2x - 4

Subtract 2x from both sides:

3x - 2x - 9 = 2x - 2x - 4

Simplify:

x - 9 = -4

Add 9 to both sides:

x - 9 + 9 = -4 + 9

Simplify:

x = 5

So, the solution for the 3(x - 3) = 2(x - 2) is x = 5.

`\hrulefill`

`\sf 3)\:\: (4)/(3 )= x + (3)/(4)`

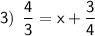
Subtract
`\sf (1)/(3)` from both sides:

`\sf (4)/(3) - (3)/(4 )= x + (3)/(4) - (3)/(4)`

Find the common denominator (12):

`\sf (4*4-3*3)/(12)=x`

`\sf ((16 - 9))/(12) = x`

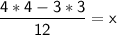
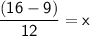
Simplify:

`\sf (7)/(12) = x`

So, the solution for the
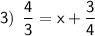`\sf 3)\:\: (4)/(3 )= x + (3)/(4)` is
`\sf x =(7)/(12)`

`\hrulefill`

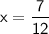
4) 10x + 5(x + 5)

Distribute 5: 10x + 5x + 25

Combine like terms: 15x + 25

So, the fourth equation is already simplified and does not have a single solution for x. It represents the expression 15x + 25.

Exceptional:

4) If the equation is:

10x = 5(x + 5)

Distribute the 5 on the right side of the equation:

10x = 5x + 25

Subtract 5x from both sides to isolate the x term on the left side:

10x - 5x = 5x - 5x + 25

Simplify the equation:

5x = 25

divide both sides by 5 to solve for x:

`\sf x = (25)/(5)`

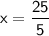
simplify the result:

x = 5

So, the solution for the equation 10x = 5(x + 5) is x = 5.