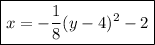Answer:
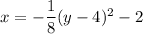
Explanation:
To find the equation for the parabola with the given focus and vertex, we can use the form:
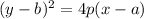
where
 is the vertex and
is the vertex and
 is the distance from the focus to the vertex, with respect to direction (right is a positive distance, left is a negative distance).
is the distance from the focus to the vertex, with respect to direction (right is a positive distance, left is a negative distance).
We are given that the vertex is:

Therefore, we can assign the following variable values:
We can see that the focus is 2 units to the left of the vertex. Therefore, we can assign the following value for the variable
 :
:
Using these values, we can form the equation:
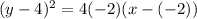
which can be simplified to solve for
 .
.
↓ rewriting subtraction of a negative as addition of a positive
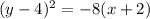
↓ applying the distributive property ...

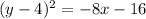
↓ adding 16 to both sides
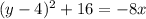
↓ dividing both sides by -8
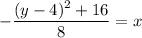
This can be rewritten with two terms on the side with
 as:
as: