Question

Find the angle between the vectors v = (2, 4) and w = (-3, 1).

Answer 1

≈ 98°

Explanation:

the angle between 2 vectors is calculated as

cosθ =
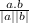`(a.b)/(|a||b|)` ( θ is the angle between the vectors a and b )

a • b ← is the dot product and

| a | , | b | ← is the magnitude of the 2 vectors

given

v = (2, 4 ) and w = (- 3, 1 )

then

v • w = (2 × - 3) + (4 × 1) = - 6 + 4 = - 2 , and

| v | =
`√(2^2+4^2)` =
`√(4+16)` =
`√(20)`

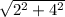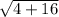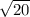
| w | =
`√((-3)^2+1^2)` =
`√(9+1)` =
`√(10)`

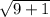substitute these values into the formula for cosθ

cosθ =
`\frac{-2}{\sqrt{20(√(10)) } }` =
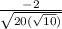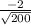`(-2)/(√(200) )` , then

θ =
`cos^(-1)` (
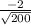`(-2)/(√(200) )` ) ≈ 98° ( to the nearest degree )