Question

Suppose that $2000 is loaned at a rate of 12.5%, compounded quarterly. Assuming that no payments are made, find the amount owed after 6 years.

Do not round any intermediate computations, and round your answer to the nearest cent.

Answer 1

First, you must set up the equation for Annual Compound Interest and identify your associated variables:

`A = P (1 + r/n) ^(nt)`

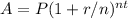
• A= Final value (including interest)
• P = principal/original amount: $2000
• r = rate as a decimal: 0.125
• n= number of times compounded yearly: quarterly: 4
• t= numbers of years borrowed for: 6

Now, plug in the information you know into your equation:

`A= 2000 (1 +(0.125)/(4) )^((4)(6))`

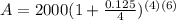
Now, solve for A:

`A= 2000 (1 +(0.03125)/(4) )^((4)(6))`

`A= 2000 (1.03125 )^((4)(6))`

`A= 2000 (1 .03125} )^((20))`

`A= 2000 (1 .850457995)}`

`A= 3700.915`

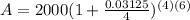
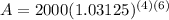
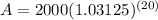
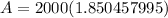
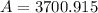
Round your answer to the nearest cent, and you should get around $3700.00 as your final answer