Question

Write the factored from of each trinomial x^2+15x+54

Answer 1

(x + 6)(x + 9)

Explanation:

x² + 15x + 54

consider the factors of the constant term (+ 54) which sum to give the coefficient of the x- term (+ 15)

the factors are + 6 and + 9 , since

+ 6 × + 9 = + 54 and + 6 + 9 = 15 ,then

x² + 15x + 54 = (x + 6)(x + 9) ← in factored form

Answer 2

Factored form is
`\sf (x+9)(x+6)`

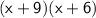
Explanation:

`\sf x^2+15x+54`

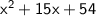
We can factor it by middle term factorization:

Let's find two integers whose product is 54 and whose sum is 15.

• The factors of 54 are 1, 2, 3, 6, 9, 18, 27, and 54.

• The only two factors whose sum is 15 are 9 and 6.

So, we can write the above equation as,

`\sf x^2 + (9+6)x + 54`

`\sf x^2 +9x+6x +54`

Taking common from each term

`\sf x(x+9)+6(x+9)`

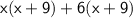
Taking common and keeping remaining in bracket

`\sf (x+9)(x+6)`

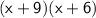
Therefore, the factored form of
`\sf x^2+15x+54 \:\:is \:\: \bold{(x + 9)(x + 6).}`