Question

Help needed urgently, i tried to solve it but couldn't get it right

Answer 1

• Angle ESH = 107°

• Angle HRE = 73°

Explanation:

A cyclic quadrilateral is a quadrilateral that can be inscribed in a circle, meaning that all four vertices of the quadrilateral lie on the same circle. Cyclic quadrilaterals have a number of properties that are not shared by other quadrilaterals.

Some of the properties of cyclic quadrilaterals include:

• The sum of the opposite angles of a cyclic quadrilateral is always 180 degrees.
• The diagonals of a cyclic quadrilateral bisect each other at right angles.
• The product of the diagonals of a cyclic quadrilateral is equal to the sum of the products of the opposite sides.
• The area of a cyclic quadrilateral can be found using Brahmagupta's formula.

In this case:

We use the property:

The sum of the opposite angles of a cyclic quadrilateral is always 180 degrees.

So,

`\sf (2x+7) ^\circ+(x+23)^\circ = 180^\circ`

Solving like terms

`\sf 2x+7+x+23= 180`

`\sf \sf 3x +30 =180`

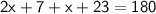
Subtracting both sides by 30.

`\sf 3x = 180 - 30`

`\sf 3x = 150`

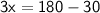
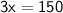
Dividing both sides by 3, we get

`\sf x =(150)/(3)`

`\sf x =50`

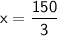
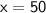
Now,

m ∡ ESH =
`\sf (2x+7)^\circ = (2*50+7)^\circ = 107^\circ`

m ∡ HRE =
`\sf (x+23)^\circ = (50+23)^\circ =73 ^\circ`

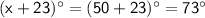
Therefore,

• Angle ESH = 107°

• Angle HRE = 73°