Question

Hi can I please have help with this problem? Thank you!!

Answer 1

Hyperbola (vertical)

Explanation:

Given conic section equation:

`5x^2-11y^2-26x+2y+36=0`

The general equation for any conic section is:

`\boxed{Ax^2+Bxy+Cy^2+Dx+Ey+F=0}`

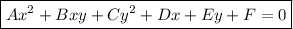
where A, B, C, D, E and F are constants.

If B² − 4AC < 0, if a conic exists, it will be either a circle or an ellipse.
(If A = C and B = 0, the equation represents a circle).

If B² − 4AC = 0, if a conic exists, it will be a parabola.

If B² − 4AC > 0, if a conic exists, it will be a hyperbola.

For the given equation, the coefficients of A, B and C are:

• A = 5
• B = 0
• C = -11

Substitute the coefficients into B² − 4AC:

`\begin{aligned}B^2-4AC&=0^2-4(5)(-11)\\&=0-20(-11)\\&=220 > 0\end{aligned}`

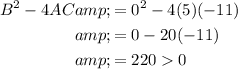
As B² − 4AC > 0, the conic is a hyperbola.

`\hrulefill`

To rewrite the given equation in the standard form of a hyperbola, we can complete the square.

Given equation:

`5x^2-11y^2-26x+2y+36=0`

Arrange the equation so all the terms with variables are on the left side and the constant is on the right side:

`5x^2-26x-11y^2+2y=-36`

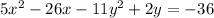
Factor out the coefficient of the x² term and the coefficient of the y² term:

`5\left(x^2-(26)/(5)x\right)-11\left(y^2-(2)/(11)y\right)=-36`

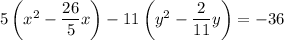
Add the square of half the coefficient of x and y inside the parentheses of the left side, and add the distributed values to the right side:

`5\left(x^2-(26)/(5)x+(169)/(25)\right)-11\left(y^2-(2)/(11)y+(1)/(121)\right)=-36+(169)/(5)-(1)/(11)`

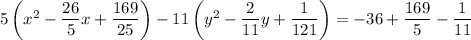
Factor the two perfect trinomials on the left side and simplify the right side:

`5\left(x-(13)/(5)\right)^2-11\left(y-(1)/(11)\right)^2=-(126)/(55)`

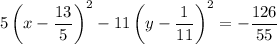
Divide both sides by the number of the right side so the right side equals 1:

`(5\left(x-(13)/(5)\right)^2)/(-(126)/(55))-(11\left(y-(1)/(11)\right)^2)/(-(126)/(55))=(-(126)/(55))/(-(126)/(55))`

`(-\left(x-(13)/(5)\right)^2)/((126)/(275))+(\left(y-(1)/(11)\right)^2)/((126)/(605))=1`

`(\left(y-(1)/(11)\right)^2)/((126)/(605))-(\left(x-(13)/(5)\right)^2)/((126)/(275))=1`

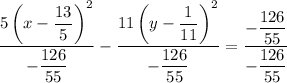
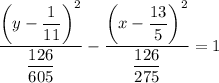
As the y²-term is positive, the hyperbola is vertical (opening up and down).