Question

An electron with a speed of 1.7 x 10^7 m/s moves horizontally into a region where a constant vertical force of 3.9x 10^-16 N acts on it The mass of the electron is 9.11 10^-31 kg. Determine the vertical distance the electron is deflected during the time it has moved 11 mm horizontally.

Answer 1

Approximately
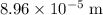`8.96 * 10^(-5)\; {\rm m}` (assuming that the effective mass of the electron is equal to its rest mass.)

Step-by-step explanation:

To find distance travelled vertically over the time the particle traversed the given horizontal distance, start by finding the duration of this motion. The vertical acceleration of the particle can be found using Newton's Laws of Motion. After both duration and acceleration are found, apply the SUVAT equations to find the vertical displacement.

Make sure all quantities are measured in standard units. Specifically, make sure the unit of the horizontal distance is in the standard unit of meters:

`\displaystyle 11\; {\rm mm} = 11\; {\rm mm} * \frac{1\; {\rm m}}{10^(3)\; {\rm mm}} = 0.011\; {\rm m}`.

Divide the horizontal displacement travelled by the horizontal velocity to find the duration of the motion:

`\begin{aligned}t &= \frac{0.011\; {\rm m}}{1.7 * 10^(7)\; {\rm m\cdot s^(-1)}} \approx 6.4706 * 10^(-10)\; {\rm s}\end{aligned}`.

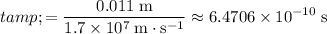Assume that the effective mass of this electron is the same as its mass
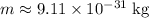`m \approx 9.11 * 10^(-31)\; {\rm kg}` when it is not moving. Divide the vertical resultant force on the electron by the effective mass of the electron to find the acceleration of the electron in the vertical direction:

`\begin{aligned}(\text{acceleration}) &= \frac{(\text{net force})}{(\text{effective mass})} \\ &\approx \frac{3.9 * 10^(-16)\; {\rm N}}{9.11* 10^(-31)\; {\rm kg}} \\ &\approx 4.2810 * 10^(14)\; {\rm m\cdot s^(-2)}\end{aligned}`.

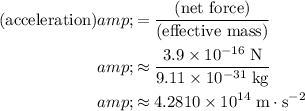Since the electron was initially moving horizontally, initial horizontal velocity of the electron would be
`u = 0\; {\rm m\cdot s^(-1)}`.

Since vertical acceleration is found to be
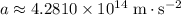`a \approx 4.2810 * 10^(14)\; {\rm m\cdot s^(-2)}`, apply the SUVAT equation
`x = (1/2)\, a\, t^(2) + u\, t` to find the vertical displacement
`x` over the given time period of
`t \approx 6.4706 * 10^(-10)\; {\rm s}`:

`\begin{aligned} x &= (1)/(2)\, a\, t^(2) + u\, t \\ &\approx (1)/(2)\, (4.2810 * 10^(14))\, (6.4706* 10^(-10))^(2)\; {\rm m} \\ &\quad + (0)\,(6.4706* 10^(-10))\; {\rm m} \\ &\approx 8.96 * 10^(-5)\; {\rm m}\end{aligned}`.

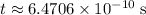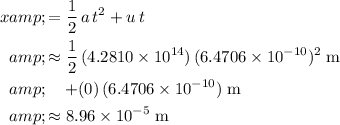In other words, the vertical displacement of the electron over the given period of time would be approximately
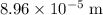`8.96 * 10^(-5)\; {\rm m}` under the assumptions.