Question

Refer to Figure 2 The magnitudes of the forces as shown in the figure are:

F1 = 80.0 N, F2 = 60.0 N, and F3 = 40.0 N. The resultant (net) vector force acting on the particle O is given by:


Please help me solve this i need it all i know is that the right answer is B

Answer 1

B) 35.5 N at an angle 34.3° with respect to +x-axis

Step-by-step explanation:

∑Fx = F₁ cos 30° - F₃

=
`80*(1)/(2) √(3) -40`

= 29.28 N

∑Fy = F₂ - F₁ sin 30°

=
`60- 80*(1)/(2)`

= 20 N

∑F² = ∑Fx² + ∑Fy²

= 29.28² + 20²

∑F = √1257.74

= 35.5 N

tan ∠F =
`(\Sigma Fy)/(\Sigma Fx)`

=
`(20)/(29.28)`

∠F = atan 0.683

= 34.3°

Answer 2

B) 35.5 N at an angle 34.3° with respect to the +x-axis.

Step-by-step explanation:

Rewrite each force in component form (where vectors are represented using the unit vectors i and j along the x and y axes):

`\mathbf{F_1}=(80.0\cos 30^(\circ))\:\mathbf{i}-(80.0\sin30^(\circ))\:\mathbf{j}=40√(3)\:\mathbf{i}-40\:\mathbf{j}`

`\mathbf{F_2}=60\:\mathbf{j}`

`\mathbf{F_3}=-40\:\mathbf{i}`

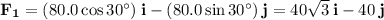
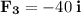
Resolve the forces:

`\mathbf{F_(net)}=\mathbf{F_1}+\mathbf{F_2}+\mathbf{F_3}`

`\mathbf{F_(net)}=(40√(3)\:\mathbf{i}-40\:\mathbf{j})+60\:\mathbf{j}+(-40\:\mathbf{i})`

`\mathbf{F_(net)}=(-40+40√(3))\:\mathbf{i}+20\:\mathbf{j}`

`\textsf{For a force\;\;$\mathbf{F} = x\mathbf{i} + y\mathbf{j}$, its magnitude is\;\;$|\mathbf{F}| = √(x^2+y^2)$.}`

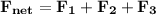
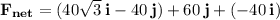
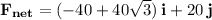
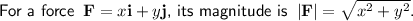
Calculate the magnitude of the resultant force:

`\begin{aligned}|\mathbf{F_(net)}|&=\sqrt{(-40+40√(3))^2+20^2}\\\\&=35.4603640...\\\\&=35.5\; \rm N\; \sf (3\;s.f.)\end{aligned}`

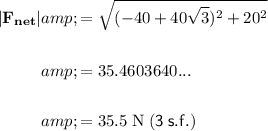
The direction θ can be found by finding the angle with the horizontal, which is given by:

`\boxed{\theta=\tan^(-1)\left((y)/(x)\right)}`

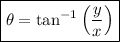
Note that tan⁻¹(y/x) will be the direction θ when 0 < θ < 90°.

When θ is between 90° and 360°, we may need to add or subtract this angle to/from 180° or 360°.

The values of x and y are:

`x=(-40+40√(3))`

`y=20`

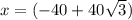
As both values are positive, the resultant vector lies in quadrant I, so we can simply calculate θ (without the need to add or subtract the angle to or from 180° or 360°).

Therefore:

`\theta=\tan^(-1)\left((20)/(-40+40√(3))\right)`

`\theta=34.3335723...^(\circ)`

`\theta=34.3^(\circ)\; \sf (3\;s.f.)`

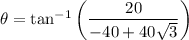
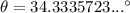
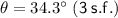
Therefore, the resultant (net) vector force acting on the particle O is given by 35.5 N at an angle 34.3° with respect to the +x-axis.