Question

!50 POINTS! (3 SIMPLE GEOMETRY QUESTIONS)

QUESTIONS BELOW
|
|
\/

Answer 1

`\textsf{10)}\quad x = 30`

`\textsf{11)} \quad \textsf{c)}\;\;(x-4)^2+(y+7)^2=16`

`\textsf{12)} \quad x = 10`

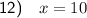
Explanation:

Question 10

The given diagram shows a circle with two tangents segments drawn to the circle from an exterior point. The major intercepted arc is labelled as 210°. As the sum of the major arc and the minor arc is 360°, the measure of the minor intercepted arc is 150°.

If two tangent segments are drawn from an exterior point to a circle, the measure of the angle formed by the two lines is half of the (positive) difference of the measures of the intercepted arcs.

Therefore:

`x^(\circ)=(1)/(2)\left|210^(\circ)-150^(\circ)\right|`

`x^(\circ)=(1)/(2)\cdot 60^(\circ)`

`x^(\circ)=30^(\circ)`

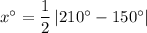
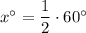
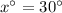
Therefore, the value of x is 30.

`\hrulefill`

Question 11

The general formula for the equation of a circle is:

`\boxed{(x-h)^2+(y-k)^2=r^2}`

where:

• (h, k) is the center.
• r is the radius.

Given the center of a circle is (4, -7) and its radius is 4 units, then:

• h = 4
• k = -7
• r = 4

Substitute the values of h, k and r into the formula to create the equation of the circle:

`(x-4)^2+(y-(-7))^2=4^2`

`(x-4)^2+(y+7)^2=16`

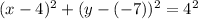
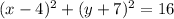
Therefore, the equation of the circle is:

`\large\boxed{(x-4)^2+(y+7)^2=16}`

`\hrulefill`

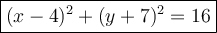
Question 12

According to the Angles of Intersecting Chords Theorem, if two chords intersect within a circle, the measure of each angle formed is equal to half the sum of the measures of the intercepted arcs on the circle. Therefore:

`\begin{aligned}60^(\circ)&=(1)/(2)\left[(4x+7)^(\circ)+(6x+13)^(\circ)\right]\\\\60&=(1)/(2)\left(10x+20\right)\\\\60&=5x+10\\\\60-10&=5x+10-10\\\\50&=5x\\\\(50)/(5)&=(5x)/(5)\\\\10&=x\end{aligned}`

Therefore, the value of x is 10.