Question

!50 POINTS! (3 SIMPLE GEOMETRY QUESTIONS)

QUESTIONS BELOW
|
|
\/

Answer 1

13) 1. a, 2. b, 3. c

14) x = 52.5°

15) x = 5

Explanation:

Question 13

The given diagram shows a circle with two intersecting chords.

The Angles of Intersecting Chords Theorem states that if two chords intersect within a circle, the measure of each angle formed is equal to half the sum of the measures of the intercepted arcs on the circle.

Therefore, according to the Angles of Intersecting Chords Theorem:

`\begin{aligned}x^(\circ)&=(1)/(2)\left(176^(\circ)+110^(\circ)\right)\\\\x^(\circ)&=(1)/(2)\cdot 286^(\circ)\\\\x^(\circ)&=143^(\circ)\end{aligned}`

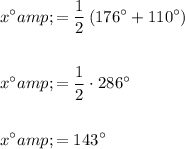
Angles x and z form a linear pair, meaning that their sum is 180°. Therefore:

`\begin{aligned}z^(\circ)+x^(\circ)&=180^(\circ)\\\\z^(\circ)+143^(\circ)&=180^(\circ)\\\\z^(\circ)&=37^(\circ)\\\\\end{aligned}`

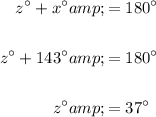
Now we know the measure of angle z, we can apply the Angles of Intersecting Chords Theorem to find the measure of angle y.

`\begin{aligned}z^(\circ)&=(1)/(2)\left(54^(\circ)+y^(\circ)\right)\\\\37^(\circ)&=(1)/(2)\left(54^(\circ)+y^(\circ)\right)\\\\74^(\circ)&=54^(\circ)+y^(\circ)\\\\y^(\circ)&=20^(\circ)\end{aligned}`

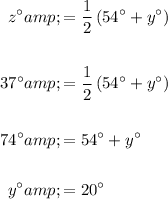
Therefore:

• x° = 143°
• y° = 20°
• z° = 37°

`\hrulefill`

Question 14

The given diagram shows a circle with a tangent line and a secant line, intersecting at an exterior point.

To find the measure of angle x, we can use the Intersecting Secant-Tangent Theorem.

The Intersecting Secant-Tangent Theorem states that if a tangent segment and a secant segment are drawn to a circle from one exterior point, then the measure of the angle formed by the two lines is half of the (positive) difference of the measures of the intercepted arcs.

Before we apply the Intersecting Secant-Tangent Theorem to find the measure of angle x, we need to calculate the measure of the unlabelled minor arc. As the sum of all arc measures of a circle is 360°, then the measure of the unlabelled minor arc is:

`360^(\circ)-167^(\circ)-149^(\circ)=44^(\circ)`

Now apply the Intersecting Secant-Tangent Theorem to find the measure of angle x:

`\begin{aligned}x^(\circ)&=(1)/(2) \left| 149^(\circ)-44^(\circ) \right|\\\\x^(\circ)&=(1)/(2) \cdot 105^(\circ) \\\\x^(\circ)&=52.5^(\circ)\end{aligned}`

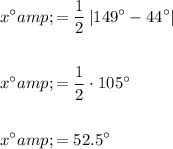
Therefore, the measure of angle x is 52.5°.

`\hrulefill`

Question 15

The given diagram shows a circle with two intersecting chords.

The Intersecting Chords Theorem states that when two chords intersect inside a circle, the product of the lengths of the segments of one chord is equal to the product of the lengths of the segments of the other chord.

Therefore:

`\begin{aligned}3x \cdot 2x&=30 \cdot 5\\\\6x^2&=150\\\\x^2&=(150)/(6)\\\\x^2&=25\\\\√(x^2)&=√(25)\\\\x&=5\end{aligned}`

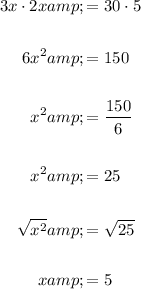
Therefore, the value of x is 5.