Question

Consider the vector field:

F(x, y, z) = (x^2 * y) * i + (2 * y^2 * z) * j + (3 * x * z^2) * k

Find the line integral of F along the curve C, parameterized by:

x = t^2, y = t^3, z = t

where t ranges from 0 to 1.

Answer 1

64/45

Explanation:

Given vector field:

`\mathbf{F}(x, y, z) = (x^2y)\mathbf{i} + (2 y^2z)\mathbf{j} + (3 x z^2) \mathbf{k}`

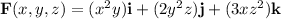
To find the line integral of the given vector field along the curve C parameterized by x = t², y = t³, z = t, where 0 ≤ t ≤ 1, we need to evaluate the line integral using the given parameterization.

`\textsf{The line integral of a vector field $\mathbf{F}$ along a curve $C$ parameterized by}`

`\textsf{$r(t) = x(t)\mathbf{i} + y(t)\mathbf{j} + z(t)\mathbf{k}$\;\;from\;\;$t=a$\;to\;$t=b$\;\;is\;given\;by:}`

`\large\boxed{\displaystyle \int_C \mathbf{F} \cdot d\mathbf{r} = \int_a^b \mathbf{F}(\mathbf{r}(t)) \cdot \mathbf{r}'(t) \;dt}`

`\textsf{where\;\;$\mathbf{r}'(t)$\;\;is\;the\;derivative\;of\;\;$\mathbf{r}(t)$\;\;with\;respect\;to\;$t$.}`

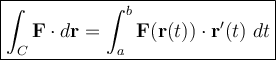
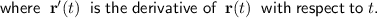
Evaluate the vector field along the curve by substituting the parameterizations into the vector field:

`\mathbf{F}(\mathbf{r}(t)) = ((t^2)^2(t^3))\mathbf{i} + (2 (t^3)^2t)\mathbf{j} + (3 (t^2) t^2) \mathbf{k}`

`\mathbf{F}(\mathbf{r}(t)) = t^7\mathbf{i} + 2t^7\mathbf{j} + 3t^4\mathbf{k}`

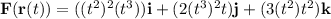
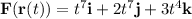
The parameterization is:

`\mathbf{r}(t) = t^2\mathbf{i} + t^3\mathbf{j} + t\mathbf{k}`

Differentiate the parameterization:

`\mathbf{r}'(t) = 2t\mathbf{i} + 3t^2\mathbf{j} + \mathbf{k}`

Now, we can evaluate the line integral by substituting the values of F(r(t)) and r'(t) into the formula:

`\displaystyle \int_C \mathbf{F} \cdot d\mathbf{r} = \int_0^1 \left( t^7\mathbf{i} + 2t^7\mathbf{j} + 3t^4\mathbf{k}\right) \cdot \left(2t\mathbf{i} + 3t^2\mathbf{j} + \mathbf{k}\right) \; dt`

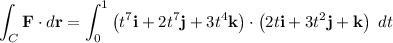
Take the dot product:

`\displaystyle \int_C \mathbf{F} \cdot d\mathbf{r} = \int_0^1 \left(t^7 \cdot 2t + 2t^7 \cdot 3t^2 + 3t^4 \cdot 1\right) \;dt`

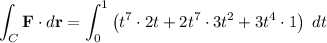
Simplify and integrate:

`\begin{aligned}\displaystyle \int_C\mathbf{F}\cdot d\mathbf{r}&=\int_0^1 \left(2t^8+6t^9+3t^4\right)\;dt\\\\&=\left[(2t^(8+1))/(8+1)+(6t^(9+1))/(9+1)+(3t^(4+1))/(4+1)\right]^1_0\\\\&=\left[(2t^(9))/(9)+(6t^(10))/(10)+(3t^(5))/(5)\right]^1_0\\\\&=\left[(2t^(9))/(9)+(3t^(10))/(5)+(3t^(5))/(5)\right]^1_0\\\\\end{aligned}`

`\begin{aligned}&=\left((2(1)^(9))/(9)+(3(1)^(10))/(5)+(3(1)^(5))/(5)\right)-\left((2(0)^(9))/(9)+(3(0)^(10))/(5)+(3(0)^(5))/(5)\right)\\\\&=(2)/(9)+(3)/(5)+(3)/(5)\\\\&=(64)/(45)\end{aligned}`

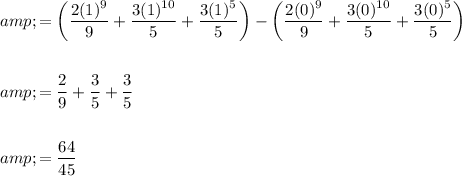
Therefore, the line integral of the vector field F along the curve C is 64/45.