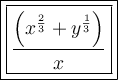Answer:

Explanation:
Given rational expression:
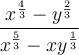
To simplify the given expression, we can first simplify the numerator and denominator separately.
Numerator
Rewrite the exponents of the terms in the numerator as:
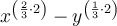
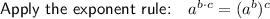
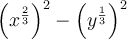
Apply the difference of two squares: a² - b² = (a + b)(a - b)
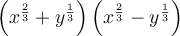
Denominator
Rewrite the exponent of the first term:
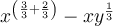
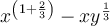


Factor out the common term x:

Therefore, after simplifying the numerator and denominator, the expression can be rewritten as:
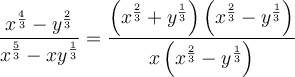
Notice that the numerator and denominator have a common factor.
Cancel the common factor:
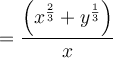
So, the simplified expression is: