Question

Identify problem: Identify the problem(s) to be solved.

Describe plan: Explain the skill/process/method you will use to solve the problem(s)
and give a brief overview.
Explain work: Describe in detail, the step by step process of how the problems are
completed and explain WHY each step is being completed.
Final answer: Clearly state the final answer of problem(s).

Answer 1

x = -2, x = 5

Explanation:

The problem is about solving for x.

This question is all about algebraic fractions and will require some factorising and manipulation.

First start by factorising the denominator on the RHS to get (x+1)(x-1).

Now in order to solve for x, we need to get rid of any fractions. To do this, we can multiply by the LCM of the denominators which is (x+1)(x-1):

`(3x(x+1)(x-1))/(x+1) - 2(x+1)(x-1) = (12(x+1)(x-1))/((x+1)(x-1))`

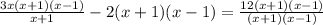
Now we can cancel some of the brackets in the fractions to get:

`3x(x-1) - 2(x^(2)-1) = 12`

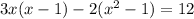
After some expanding and simplifying we get:

`x^(2) - 3x-10=0\\`

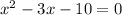
Which factorises to:

`(x+2)(x-5) = 0\\`

Therefore x = -2 or x = 5