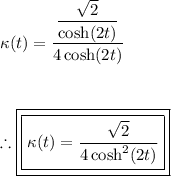Answer:
(a)
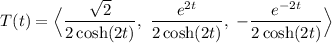
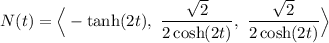
(b)
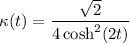
Explanation:
Part (a): Finding the unit tangent and unit normal vectors T(t) and N(t):
To find the unit tangent vector, T(t), we first need to compute the derivative of the vector function r(t) with respect to t:
![r(t) = \big < 2t√(2), \ e^(2t), \ e^(-2t) \big > \\\\\\\\\Longrightarrow r'(t) = \big < (d)/(dt)[2t√(2)], \ (d)/(dt)[e^(2t)], \ (d)/(dt)[e^(-2t)]\big > \\\\\\\\\Longrightarrow \boxed{r'(t)= \big < 2√(2), \ 2e^(2t), \ -2e^(-2t)\big > }](https://img.qammunity.org/2024/formulas/mathematics/college/ikos6mckqu86cqbh66tcjjn3auhsin0j5k.png)
Next, we find the magnitude (or length) of the vector r'(t) by taking the square root of the sum of the squares of its components:
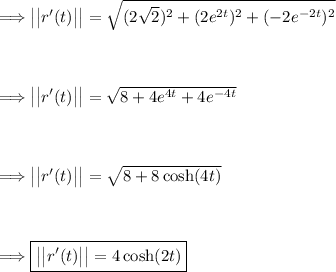
Now, we can calculate the unit tangent vector T(t) by dividing the vector r'(t) by its magnitude:


To find the unit normal vector N(t), we differentiate the unit tangent vector T(t) with respect to t:
![T(t) = \Big < (\sqrt2)/(2\cosh(2t)), \ (e^(2t))/(2\cosh(2t)), \ -(e^(-2t))/(2\cosh(2t)) \\\\\\\\\Longrightarrow T'(t) = \Big < (d)/(dt) \Big[(√(2))/(2\cosh(2t))\Big], \ (d)/(dt)\Big[(e^(2t))/(2\cosh(2t))\Big], \ (d)/(dt) \Big[-(e^(-2t))/(2\cosh(2t))\Big]\Big >](https://img.qammunity.org/2024/formulas/mathematics/college/xvd4iwrfll8d4aau4dpzrohgal34c34zeu.png)
Finding T'_x(t):

Finding T'_y(t):

Finding T'_z(t):

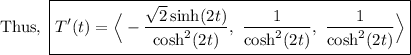
Again, we calculate the magnitude of the vector T'(t):
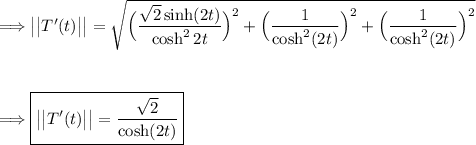
Finally, the unit normal vector N(t) is given by dividing T'(t) by its magnitude:

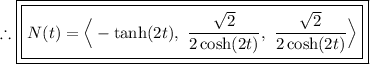

Part (b): Finding the curvature using the formula κ(t) = ||T'(t)|| / ||r'(t)||:
The curvature of a vector function r(t) is given by the formula:

We have already calculated ||T'(t)|| and ||r'(t)|| in part (a):

Now, we can plug these values into the curvature formula: