Question

Can someone please help me out?

Answer 1

`S = 2\sinh(5) \ or \ S= e^5-e^(-5)`

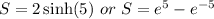
Explanation:

To find the length of the curve defined by the vector function r(t) = (√2t)i + (e^t)j + (e^(-t))k, where 0 ≤ t ≤ 5, we'll use the concept of arc length.

Arc length represents the length of a curve in a three-dimensional space. For a vector function r(t) = <x(t), y(t), z(t)>, the arc length formula for a given interval [a, b] is given by the integral of the magnitude of the derivative of r(t) with respect to t.

The formula for the arc length of the curve is:

`\boxed{\left\begin{array}{ccc}\text{\underline{Arc Length: }}\\\\\displaystyle S = \int\limits^b_a r'(t)\big \, dt \end{array}\right}`

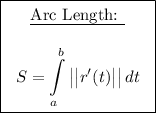
Where r'(t) is the derivative of the vector function r(t) with respect to t, and ||r'(t)|| represents its magnitude.

Let's find the derivative of r(t) and its magnitude step by step:

`\hrulefill`

(1) - Finding the derivative of r(t).
To find r'(t), we differentiate each component of the vector function with respect to t:

`r(t) = (√(2)t ) \hat i + (e^t) \hat j +(e^(-t)) \hat k\\\\\\\\ \Longrightarrow (dr(t))/(dt) = ((d)/(dt) [√(2)t]) \hat i + ((d)/(dt)[e^t]) \hat j +((d)/(dt)[e^(-t)]) \hat k\\\\\\\\\Longrightarrow \boxed{r'(t) = (√(2) ) \hat i + (e^t) \hat j +(-e^(-t)) \hat k}`

(2) - Finding the magnitude of r'(t).

The magnitude of r'(t) can be computed as follows:

`\big|\big| r'(t) \big|\big|= √((x'(t))^2+(y'(t))^2+(z'(t))^2)\\\\\\\\\Longrightarrow \big|\big| r'(t) \big|\big|= \sqrt{(√(2))^2+(e^t)^2+(-e^(-t))^2}\\\\\\\\\Longrightarrow \big|\big| r'(t) \big|\big|= \sqrt{2+e^(2t)+e^(-2t)} \\\\\\\\\Longrightarrow \big|\big| r'(t) \big|\big|= √(2+2\cosh(2t))\\\\\\\\\Longrightarrow \boxed r'(t) \big`

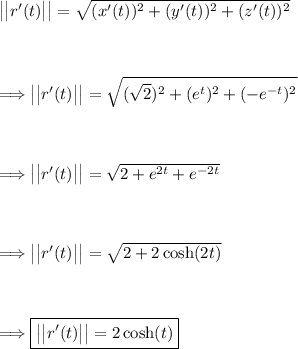
(3) - Finding the arc length.

Now, we have the expression for the magnitude of the derivative ||r'(t)||. We need to integrate it over the interval [0, 5] to find the arc length S:

`\Longrightarrow \displaystyle S= \int\limits^5_0 {(2\cosh(t))} \, dt \\\\\\\\\Longrightarrow S= \displaystyle 2\int\limits^5_0 {\cosh(t)} \, dt`

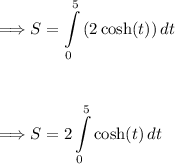
The integral of the hyperbolic cosine function, cosh(x), can be found using the following rule:

`\boxed{\left\begin{array}{ccc}\text{\underline{Hyperbolic Cosine Rule:}}\\\\\displaystyle \int {\cosh(x)} \, dx = \sinh(x) \end{array}\right}`

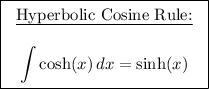
`\Longrightarrow S = 2\Big[\sinh(t)\Big]\limits^5_0\\\\\\\\\Longrightarrow S = 2\Big[\sinh(5)- \sinh(0)\Big]\\\\\\\\\Longrightarrow S = 2\Big[\sinh(5)-0\Big]\\\\\\\\ \therefore \boxed{\boxed{S = 2\sinh(5)}} \ or \ \boxed{\boxed{S= e^5-e^(-5)}}`

Thus, the length of the curve is found.

`\hrulefill`

Additional information:

Arc Length: Arc length is the length of a curve in a two-dimensional or three-dimensional space. It measures the distance along the path traced by the curve and can be computed by integrating the magnitude of the derivative of the curve's parametric equations with respect to the parameter over a specified interval. Arc length is used in various fields such as calculus, geometry, physics, and engineering to quantify the length of non-straight curves and paths.

Hyperbolic Functions: Hyperbolic functions are a set of mathematical functions that are analogs to trigonometric functions but are defined using exponential functions. The three primary hyperbolic functions are:

`\boxed{\left\begin{array}{ccc}\text{\underline{Hyperbolic Functions:}}\\\\\bullet \ \text{Hyperbolic Sine:} \ \sinh(t)=(e^t-e^(-t))/(2)\\\\\bullet \ \text{Hyperbolic Cosine:} \ \cosh(t)=(e^t+e^(-t))/(2) \\\\ \bullet \ \text{Hyperbolic Tangent:} \ \tanh(t)=(e^t-e^(-t))/(e^t+e^(-t)) \end{array}\right }`

There are also hyperbolic functions for cosecant (csch(t)), secant (sech(t)), and cotangent (coth(t)).

The definitions of hyperbolic functions involve exponential terms, making them related to the exponential function and its properties. These functions are essential in many areas of mathematics and science and have their own unique characteristics and applications.