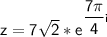2 Answers

Suszterpatt · Answer 1 · 2024-01-28T12:54:27+0000

Answer:

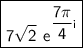
$\boxed{\sf 7√(2) \:\:e^{(7\pi )/( 4)i}}$

Explanation:

To rewrite the complex number 7 - 7i into polar form re^(iθ), we need to find the magnitude (r) and argument (θ) of the complex number.

Magnitude (r):

The magnitude (r) of a complex number a + bi is given by the square root of the sum of the squares of its real and imaginary parts:

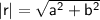
$\sf |r| = √(a^2 + b^2)$

In this case, a = 7 and b = -7, so:

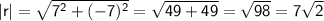
$\sf |r| = √(7^2 + (-7)^2) = √(49 + 49)= √(98) = 7√(2)$

Argument (θ):

The argument (θ) of a complex number a + bi in the polar form is given by the arctangent of the imaginary part divided by the real part:

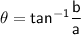
$\sf \theta = tan^(-1)(b)/(a)$

In this case, a = 7 and b = -7, so:

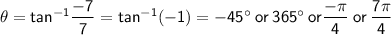
$\sf \theta= tan^(-1)(-7)/(7) = tan^(-1)(-1)= -45^\circ\: or \: 365^\circ \:or (-\pi)/(4) \:or\:(7\pi)/(4)$

So the complex number 7 - 7i in polar form
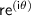$\sf re^((i\theta) )$ is:

$\sf z =7√(2) * e^(7\pi)/(4) i$

Please log in or register to add a comment.